Očito, u slučaju vektorskog produkta, bitan je redoslijed kojim su vektori uzeti, štoviše,

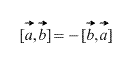
Također, izravno iz definicije slijedi da za bilo koji skalarni faktor k (broj) vrijedi sljedeće:

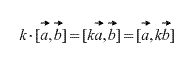
Vektorsko umjetničko djelo kolinearni vektori jednak nultom vektoru. Štoviše, umnožak dvaju vektora jednak je nuli ako i samo ako su kolinearni. (U slučaju da je jedan od njih nulti vektor, potrebno je zapamtiti da je nulti vektor kolinearan svakom vektoru po definiciji).

Vektorski proizvod ima raspodjelna svojina, odnosno

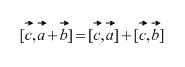
Izražavanje vektorskog umnoška preko koordinata vektora.

Neka su dana dva vektora

(kako pronaći koordinate vektora iz koordinata njegovog početka i kraja - vidi članak Točkasti umnožak vektora, točka Alternativna definicija točkastog umnoška ili izračunavanje točkastog umnoška dvaju vektora zadanih njihovim koordinatama.)

Zašto vam je potreban vektorski proizvod?

Postoji mnogo načina za korištenje križnog produkta, na primjer, kao što je gore napisano, izračunavanjem križnog produkta dvaju vektora možete saznati jesu li kolinearni.

Ili se može koristiti kao način za izračunavanje površine paralelograma konstruiranog od ovih vektora. Na temelju definicije, duljina rezultirajućeg vektora je površina zadanog paralelograma.

Također ogroman iznos primjene postoje u elektricitetu i magnetizmu.

Online kalkulator vektorskih proizvoda.

Da biste pomoću ovog kalkulatora pronašli skalarni umnožak dvaju vektora, trebate unijeti u prvi red redom koordinate prvog vektora, u drugi - drugi. Koordinate vektora mogu se izračunati iz koordinata njihovog početka i kraja (vidi članak Točkasti umnožak vektora, stavka Alternativna definicija točkastog umnoška ili izračunavanje točkastog umnoška dvaju vektora zadanih njihovim koordinatama.)

Prije nego što damo koncept vektorskog produkta, okrenimo se pitanju orijentacije uređene trojke vektora a →, b →, c → u trodimenzionalnom prostoru.

Za početak ostavimo po strani vektore a → , b → , c → iz jedne točke. Orijentacija trojke a → , b → , c → može biti desna ili lijeva, ovisno o smjeru samog vektora c →. Tip trojke a → , b → , c → odredit ćemo iz smjera u kojem je napravljen najkraći zavoj od vektora a → do b → od kraja vektora c → .

Ako se najkraći zaokret izvede u smjeru suprotnom od kazaljke na satu, tada se trojka vektora a → , b → , c → naziva pravo, ako u smjeru kazaljke na satu – lijevo.

Zatim uzmite dva nekolinearna vektora a → i b →. Nacrtajmo zatim vektore A B → = a → i A C → = b → iz točke A. Konstruirajmo vektor A D → = c →, koji je istovremeno okomit na A B → i A C →. Dakle, kada konstruiramo sam vektor A D → = c →, možemo to učiniti na dva načina, dajući mu jedan ili suprotan smjer (vidi sliku).

Uređena trojka vektora a → , b → , c → može biti, kako smo saznali, desna ili lijeva ovisno o smjeru vektora.

Iz navedenog možemo uvesti definiciju vektorskog produkta. Ova definicija dana je za dva vektora definirana u pravokutnom koordinatnom sustavu trodimenzionalnog prostora.

Definicija 1

Vektorski produkt dva vektora a → i b → nazvat ćemo takav vektor definiran u pravokutnom koordinatnom sustavu trodimenzionalnog prostora tako da je:

• ako su vektori a → i b → kolinearni, bit će nula;
• bit će okomit na vektor a → ​​​​ i na vektor b → tj. ∠ a → c → = ∠ b → c → = π 2 ;
• duljina mu je određena formulom: c → = a → · b → · sin ∠ a → , b → ;
• trojka vektora a → , b → , c → ima istu orijentaciju kao zadani koordinatni sustav.

Vektorski produkt vektora a → i b → ima sljedeću oznaku: a → × b →.

Koordinate vektorskog umnoška

Budući da svaki vektor ima određene koordinate u koordinatnom sustavu, možemo uvesti drugu definiciju vektorskog produkta, koja će nam omogućiti da pronađemo njegove koordinate pomoću zadanih koordinata vektora.

Definicija 2

U pravokutnom koordinatnom sustavu trodimenzionalnog prostora vektorski produkt dvaju vektora a → = (a x ; a y ; a z) i b → = (b x ; b y ; b z) naziva se vektor c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , gdje su i → , j → , k → koordinatni vektori.

Vektorski umnožak može se prikazati kao determinanta kvadratne matrice trećeg reda, pri čemu prvi red sadrži vektorske vektore i → , j → , k → , drugi red sadrži koordinate vektora a → , a treći redak sadrži koordinate vektora b → u zadanom pravokutnom koordinatnom sustavu, to je determinanta matrice koja izgleda ovako: c → = a → × b → = i → j → k → a x a y a z b x b y b z

Proširujući ovu determinantu na elemente prvog retka, dobivamo jednakost: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · i → - a x a z b x b z · j → + a x a y b x b y · k → = = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →

Svojstva križnog umnoška

Poznato je da se vektorski umnožak u koordinatama predstavlja kao determinanta matrice c → = a → × b → = i → j → k → a x a y a z b x b y b z , tada na temelju svojstva determinante matrice prikazuju se sljedeće svojstva vektorskog proizvoda:

1. antikomutativnost a → × b → = - b → × a → ;
2. distributivnost a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → ili a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
3. asocijativnost λ a → × b → = λ a → × b → ili a → × (λ b →) = λ a → × b →, gdje je λ proizvoljan realan broj.

Ova svojstva imaju jednostavne dokaze.

Kao primjer, možemo dokazati antikomutativno svojstvo vektorskog produkta.

Dokaz antikomutativnosti

Po definiciji, a → × b → = i → j → k → a x a y a z b x b y b z i b → × a → = i → j → k → b x b y b z a x a y a z . A ako se dva retka matrice zamijene, tada bi se vrijednost determinante matrice trebala promijeniti u suprotnu, dakle, a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → , što i dokazuje da je vektorski produkt antikomutativan.

Vektorski proizvod - primjeri i rješenja

U većini slučajeva postoje tri vrste problema.

U zadacima prvog tipa obično su zadane duljine dvaju vektora i kut između njih, a potrebno je pronaći duljinu vektorskog umnoška. U ovom slučaju upotrijebite sljedeću formulu c → = a → · b → · sin ∠ a → , b → .

Primjer 1

Odredite duljinu vektorskog umnoška vektora a → i b →, ako znate a → = 3, b → = 5, ∠ a →, b → = π 4.

Otopina

Određivanjem duljine vektorskog umnoška vektora a → i b → rješavamo ovaj problem: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .

Odgovor: 15 2 2 .

Problemi drugog tipa povezani su s koordinatama vektora, u njima vektorski produkt, njegova duljina itd. pretražuju se kroz poznate koordinate zadanih vektora a → = (a x; a y; a z) I b → = (b x ; b y ; b z) .

Za ovu vrstu problema možete riješiti puno opcija zadataka. Na primjer, ne mogu se zadati koordinate vektora a → i b →, već njihova proširenja u koordinatne vektore oblika b → = b x · i → + b y · j → + b z · k → i c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →, ili se vektori a → i b → mogu odrediti koordinatama njihovog početka i krajnje točke.

Razmotrite sljedeće primjere.

Primjer 2

U pravokutnom koordinatnom sustavu zadana su dva vektora: a → = (2; 1; - 3), b → = (0; - 1; 1). Pronađite njihov križni umnožak.

Otopina

Po drugoj definiciji nalazimo vektorski produkt dvaju vektora u zadanim koordinatama: a → × b → = (a y · b z - a z · b y) · i → + (a z · b x - a x · b z) · j → + ( a x · b y - a y · b x) · k → = = (1 · 1 - (- 3) · (- 1)) · i → + ((- 3) · 0 - 2 · 1) · j → + (2 · (- 1) - 1 · 0) · k → = = - 2 i → - 2 j → - 2 k → .

Ako vektorski produkt zapišemo kroz determinantu matrice, tada rješenje ovog primjera izgleda ovako: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .

Odgovor: a → × b → = - 2 i → - 2 j → - 2 k → .

Primjer 3

Odredite duljinu vektorskog produkta vektora i → - j → i i → + j → + k →, gdje su i →, j →, k → jedinični vektori pravokutnog Kartezijevog koordinatnog sustava.

Otopina

Najprije pronađimo koordinate zadanog vektorskog umnoška i → - j → × i → + j → + k → u zadanom pravokutnom koordinatnom sustavu.

Poznato je da vektori i → - j → i i → + j → + k → imaju koordinate (1; - 1; 0), odnosno (1; 1; 1). Nađimo duljinu vektorskog produkta pomoću determinante matrice, tada imamo i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .

Stoga vektorski produkt i → - j → × i → + j → + k → ima koordinate (- 1 ; - 1 ; 2) u zadanom koordinatnom sustavu.

Duljinu vektorskog produkta nalazimo pomoću formule (pogledajte odjeljak o pronalaženju duljine vektora): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6.

Odgovor: i → - j → × i → + j → + k → = 6 . .

Primjer 4

U pravokutnom kartezijevom koordinatnom sustavu zadane su koordinate tri točke A (1, 0, 1), B (0, 2, 3), C (1, 4, 2). Pronađite neki vektor okomit na A B → i A C → istodobno.

Otopina

Vektori A B → i A C → imaju sljedeće koordinate (- 1 ; 2 ; 2) odnosno (0 ; 4 ; 1). Nakon što smo pronašli vektorski umnožak vektora A B → i A C →, očito je da je on po definiciji okomit vektor na A B → i A C →, odnosno da je to rješenje našeg problema. Nađimo ga A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .

Odgovor: - 6 i → + j → - 4 k → . - jedan od okomitih vektora.

Problemi treće vrste usmjereni su na korištenje svojstava vektorskog umnoška vektora. Nakon čije primjene ćemo dobiti rješenje zadanog problema.

Primjer 5

Vektori a → i b → su okomiti i njihove duljine su 3 odnosno 4. Odredite duljinu vektorskog umnoška 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → .

Otopina

Svojstvom distributivnosti vektorskog produkta možemo pisati 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →

Svojstvom asocijativnosti numeričke koeficijente izuzimamo iz predznaka vektorskih umnožaka u zadnjem izrazu: 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → = = 3 · a → × a → + 3 · (- 2) · a → × b → + (- 1) · b → × a → + (- 1) · (- 2) · b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →

Vektorski produkti a → × a → i b → × b → jednaki su 0, budući da je a → × a → = a → · a → · sin 0 = 0 i b → × b → = b → · b → · sin 0 = 0, tada je 3 · a → × a → - 6 · a → × b → - b → × a → + 2 · b → × b → = - 6 · a → × b → - b → × a → . .

Iz antikomutativnosti vektorskog produkta slijedi - 6 · a → × b → - b → × a → = - 6 · a → × b → - (- 1) · a → × b → = - 5 · a → × b → . .

Koristeći svojstva vektorskog umnoška, ​​dobivamo jednakost 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .

Prema uvjetu, vektori a → i b → su okomiti, odnosno kut između njih je jednak π 2. Sada sve što preostaje je zamijeniti pronađene vrijednosti u odgovarajuće formule: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → · sin (a → , b →) = 5 · 3 · 4 · sin π 2 = 60 .

Odgovor: 3 a → - b → × a → - 2 b → = 60.

Duljina vektorskog umnoška vektora po definiciji je jednaka a → × b → = a → · b → · sin ∠ a → , b → . Budući da je već poznato (iz školskog tečaja) da je površina trokuta jednaka polovici umnoška duljina njegovih dviju strana pomnoženih sa sinusom kuta između tih strana. Prema tome, duljina vektorskog produkta jednaka je površini paralelograma - dvostrukog trokuta, odnosno produkta stranica u obliku vektora a → i b →, položenih iz jedne točke, sinusom kut između njih sin ∠ a →, b →.

Ovo je geometrijsko značenje vektorskog produkta.

Fizičko značenje vektorskog umnoška

U mehanici, jednoj od grana fizike, zahvaljujući vektorskom proizvodu, možete odrediti moment sile u odnosu na točku u prostoru.

Definicija 3

Pod momentom sile F → primijenjenom na točku B, u odnosu na točku A, razumjet ćemo sljedeći vektorski produkt A B → × F →.

Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter

U ovoj lekciji ćemo pogledati još dvije operacije s vektorima: vektorski produkt vektora I mješoviti produkt vektora (odmah link za one kojima treba). U redu je, ponekad se dogodi da za potpunu sreću, osim toga skalarni produkt vektora, potrebno je sve više i više. Ovo je vektorska ovisnost. Može se činiti da ulazimo u džunglu analitičke geometrije. Ovo nije u redu. U ovom dijelu više matematike uglavnom ima malo drva, osim možda dovoljno za Pinokija. Zapravo, materijal je vrlo uobičajen i jednostavan - teško da je kompliciraniji od istog točkasti proizvod, bit će čak i manje tipičnih zadataka. Glavna stvar u analitičkoj geometriji, u što će se mnogi uvjeriti ili su se već uvjerili, jest NE POGRIJEŠITI U RAČUNANJU. Ponavljajte kao čaroliju i bit ćete sretni =)

Ako vektori svjetlucaju negdje daleko, kao munje na horizontu, nema veze, počnite s lekcijom Vektori za lutke obnoviti ili ponovno steći osnovno znanje o vektorima. Pripremljeniji čitatelji mogu se selektivno upoznati s informacijama; pokušao sam prikupiti najpotpuniju zbirku primjera koji se često nalaze u praktični rad

Što će vas odmah usrećiti? Kad sam bio mali, znao sam žonglirati s dvije ili čak tri lopte. Dobro je ispalo. Sada uopće nećete morati žonglirati, jer ćemo razmisliti samo prostorni vektori, a ravni vektori s dvije koordinate bit će izostavljeni. Zašto? Tako su se rodile ove akcije - vektor i mješoviti umnožak vektora definirani su i rade u trodimenzionalnom prostoru. Već je lakše!

Ova operacija, baš kao i skalarni umnožak, uključuje dva vektora. Neka to budu neprolazna slova.

Sama akcija označen sa kako slijedi: . Postoje i druge opcije, ali ja sam navikao vektorski umnožak vektora označavati na ovaj način, u uglatim zagradama s križićem.

I to odmah pitanje: ako je unutra skalarni produkt vektora uključena su dva vektora, a ovdje se također množe dva vektora koja je razlika? Očita razlika je prije svega u REZULTATU:

Rezultat skalarnog produkta vektora je BROJ:

Rezultat umnoška vektora je VEKTOR: , tj. množimo vektore i opet dobivamo vektor. Zatvoreni klub. Zapravo, odatle i potječe naziv operacije. U raznim obrazovna literatura oznake također mogu varirati, koristit ću slovo .

Definicija unakrsnog umnoška

Prvo će biti definicija sa slikom, a zatim komentari.

Definicija: Vektorski proizvod nekolinearni vektori, uzeti ovim redom, pod nazivom VEKTOR, duljinašto je brojčano jednaka površini paralelograma, izgrađen na ovim vektorima; vektor ortogonalno na vektore, a usmjeren je tako da baza ima pravu orijentaciju:

Raščlanimo definiciju dio po dio, ovdje ima puno zanimljivih stvari!

Dakle, mogu se istaknuti sljedeće značajne točke:

1) Izvorni vektori, označeni crvenim strelicama, prema definiciji nije kolinearna. Bit će prikladno razmotriti slučaj kolinearnih vektora malo kasnije.

2) Uzimaju se vektori po strogo određenom redoslijedu: – "a" se množi s "be", a ne "biti" s "a". Rezultat vektorskog množenja je VEKTOR, koji je označen plavom bojom. Ako vektore pomnožimo obrnutim redoslijedom, dobivamo vektor jednake duljine i suprotnog smjera (boja maline). Odnosno, jednakost je istinita .

3) Sada se upoznajmo s geometrijskim značenjem vektorskog produkta. Ovo je vrlo važna točka! DULJINA plavog vektora (a time i grimiznog vektora) brojčano je jednaka POVRŠINI paralelograma izgrađenog na vektorima. Na slici je ovaj paralelogram osjenčan crnom bojom.

Bilješka : crtež je shematski i, naravno, nominalna duljina vektorskog proizvoda nije jednaka površini paralelograma.

Prisjetimo se jedne od geometrijskih formula: Površina paralelograma jednaka je umnošku susjednih stranica i sinusa kuta između njih. Stoga, na temelju gore navedenog, vrijedi formula za izračunavanje DULJINE vektorskog produkta:

Naglašavam da se formula odnosi na DUŽINU vektora, a ne na sam vektor. Koje je praktično značenje? A značenje je da se u problemima analitičke geometrije područje paralelograma često nalazi kroz koncept vektorskog proizvoda:

Dobijmo drugu važnu formulu. Dijagonala paralelograma (crvena točkasta linija) dijeli ga na dva jednaka trokuta. Stoga se područje trokuta izgrađenog na vektorima (crveno sjenčanje) može pronaći pomoću formule:

4) Ne manje važna činjenica je da je vektor okomit na vektore, tj . Naravno, suprotno usmjereni vektor (malinasta strelica) također je okomit na izvorne vektore.

5) Vektor je usmjeren tako da osnova ima pravo orijentacija. U lekciji o prijelaz na novu osnovu Govorio sam dovoljno detaljno o ravninska orijentacija, a sada ćemo shvatiti što je prostorna orijentacija. Objasnit ću ti na prstima desna ruka . Mentalno kombinirajte kažiprst s vektorom i srednji prst s vektorom. Domali prst i mali prst pritisnite ga na dlan. Kao rezultat palac – vektorski produkt će izgledati gore. Ovo je desno orijentirana baza (to je ova na slici). Sada promijenite vektore ( kažiprst i srednji prst) na nekim mjestima, kao rezultat će se palac okrenuti, a vektorski proizvod će već gledati prema dolje. Ovo je također desno orijentirana osnova. Možda imate pitanje: koja osnova ima lijevu orijentaciju? "Dodijeliti" istim prstima lijeva ruka vektora, te dobiti lijevu bazu i lijevu orijentaciju prostora (u ovom slučaju palac će se nalaziti u smjeru donjeg vektora). Slikovito rečeno, te baze “zakreću” ili usmjeravaju prostor u različitim smjerovima. I ovaj koncept ne treba smatrati nečim nategnutim ili apstraktnim - na primjer, orijentacija prostora mijenja se najobičnijim zrcalom, a ako "izvučete reflektirani objekt iz zrcala", onda u općem slučaju to neće biti moguće kombinirati s "originalom". Usput, držite tri prsta do ogledala i analizirajte odraz ;-)

...kako je dobro da sada znaš desno i lijevo orijentirani baze, jer su izjave nekih predavača o promjeni orijentacije zastrašujuće =)

Umnožak kolinearnih vektora

Definicija je detaljno raspravljena, ostaje za vidjeti što se događa kada su vektori kolinearni. Ako su vektori kolinearni, onda se mogu postaviti na jednu ravnu liniju i naš paralelogram se također "zbraja" u jednu ravnu liniju. Područje takvog, kako kažu matematičari, degenerirati paralelogram je jednak nuli. Isto slijedi iz formule - sinus nula ili 180 stupnjeva jednak je nuli, što znači da je površina nula

Dakle, ako , onda I . Napominjemo da je sam vektorski produkt jednak nultom vektoru, ali u praksi se to često zanemaruje i piše da je i on jednak nuli.

Poseban slučaj je umnožak vektora sa samim sobom:

Pomoću vektorskog umnoška možete provjeriti kolinearnost trodimenzionalnih vektora, a mi ćemo između ostalog analizirati i ovaj problem.

Za rješavanje praktičnih primjera možda će vam trebati trigonometrijska tablica pronaći vrijednosti sinusa iz njega.

Pa, zapalimo vatru:

Primjer 1

a) Odredite duljinu vektorskog umnoška vektora ako

b) Odredite površinu paralelograma izgrađenog na vektorima ako

Otopina: Ne, ovo nije tipfeler, namjerno sam napravio iste početne podatke u rečenicama. Jer će dizajn rješenja biti drugačiji!

a) Prema stanju, trebate pronaći duljina vektor (križni produkt). Prema odgovarajućoj formuli:

Odgovor:

Ako ste upitani o duljini, tada u odgovoru navodimo dimenziju - jedinice.

b) Prema stanju, trebate pronaći kvadrat paralelogram izgrađen na vektorima. Površina ovog paralelograma brojčano je jednaka duljini vektorskog proizvoda:

Odgovor:

Napominjemo da se u odgovoru uopće ne govori o vektorskom produktu; područje figure, prema tome, dimenzija je kvadratna jedinica.

Uvijek gledamo ŠTO trebamo pronaći prema stanju i na temelju toga formuliramo jasan odgovor. Možda se čini doslovnim, ali među njima ima dosta doslovnih učitelja, a zadatak ima dobre šanse da bude vraćen na doradu. Iako se ne radi o nekoj pretjeranoj zamjerki - ako je odgovor netočan, stječe se dojam da osoba ne razumije jednostavne stvari i/ili nije shvatila bit zadatka. Ovu točku uvijek treba držati pod kontrolom pri rješavanju bilo kojeg problema iz više matematike, ali i iz drugih predmeta.

Gdje je nestalo veliko slovo "en"? U principu se moglo dodatno priložiti rješenju, ali da bih skratio unos, nisam to napravio. Nadam se da svi to razumiju i da je to oznaka za istu stvar.

Popularan primjer za DIY rješenje:

Primjer 2

Pronađite površinu trokuta izgrađenog na vektorima ako

Formula za pronalaženje površine trokuta kroz vektorski proizvod navedena je u komentarima na definiciju. Rješenje i odgovor su na kraju lekcije.

U praksi, zadatak je stvarno vrlo čest; trokuti vas općenito mogu mučiti.

Za rješavanje ostalih problema trebat će nam:

Svojstva vektorskog produkta vektora

Već smo razmotrili neka svojstva vektorskog produkta, ali ću ih uključiti u ovaj popis.

Za proizvoljne vektore i proizvoljan broj vrijede sljedeća svojstva:

1) U drugim izvorima informacija ova stavka obično nije istaknuta u svojstvima, ali je vrlo važna u praktičnom smislu. Pa neka bude.

2) – o svojstvu se također govori gore, ponekad se naziva antikomutativnost. Drugim riječima, bitan je redoslijed vektora.

3) – asocijativni odn asocijativni zakoni vektorskog produkta. Konstante se mogu lako premjestiti izvan vektorskog produkta. Stvarno, što bi tamo trebali raditi?

4) – raspodjela odn distributivni zakoni vektorskog produkta. Nema problema ni s otvaranjem zagrada.

Za demonstraciju, pogledajmo kratki primjer:

Primjer 3

Pronađite ako

Otopina: Uvjet ponovno zahtijeva pronalaženje duljine vektorskog produkta. Naslikajmo našu minijaturu:

(1) Prema asocijativnim zakonima, konstante uzimamo izvan opsega vektorskog produkta.

(2) Konstantu pomaknemo izvan modula, a modul “pojede” znak minus. Dužina ne može biti negativna.

(3) Ostalo je jasno.

Odgovor:

Vrijeme je da dodamo još drva na vatru:

Primjer 4

Izračunajte površinu trokuta izgrađenog na vektorima ako

Otopina: Pronađite površinu trokuta pomoću formule . Kvaka je u tome što su sami vektori "tse" i "de" predstavljeni kao zbrojevi vektora. Algoritam je ovdje standardan i pomalo podsjeća na primjere br. 3 i 4 lekcije Točkasti umnožak vektora. Radi jasnoće, podijelit ćemo rješenje u tri faze:

1) U prvom koraku izražavamo vektorski umnožak kroz vektorski umnožak, zapravo, izrazimo vektor pomoću vektora. Još nema riječi o duljinama!

(1) Zamijenite izraze vektora.

(2) Koristeći zakone distribucije otvaramo zagrade prema pravilu množenja polinoma.

(3) Pomoću asocijativnih zakona pomičemo sve konstante izvan vektorskih proizvoda. Uz malo iskustva, koraci 2 i 3 mogu se izvoditi istovremeno.

(4) Prvi i zadnji član jednaki su nuli (nulti vektor) zbog svojstva nice. U drugom članu koristimo svojstvo antikomutativnosti vektorskog produkta:

(5) Predstavljamo slične uvjete.

Kao rezultat toga, pokazalo se da je vektor izražen kroz vektor, što je trebalo postići:

2) U drugom koraku pronalazimo duljinu vektorskog produkta koji nam je potreban. Ova radnja je slična primjeru 3:

3) Pronađite površinu traženog trokuta:

Faze 2-3 rješenja mogle su se napisati u jednom redu.

Odgovor:

Razmatrani problem prilično je čest u testovi, evo primjera za neovisno rješenje:

Primjer 5

Pronađite ako

Kratko rješenje i odgovor na kraju lekcije. Da vidimo koliko ste bili pažljivi kada ste proučavali prethodne primjere ;-)

Umnožak vektora u koordinatama

, navedeno u ortonormirana baza , izražen formulom:

Formula je doista jednostavna: u gornji red determinante upišemo koordinatne vektore, u drugi i treći red “stavimo” koordinate vektora, te stavimo u strogom redu– prvo koordinate vektora “ve”, zatim koordinate vektora “double-ve”. Ako vektore treba pomnožiti drugačijim redoslijedom, redove treba zamijeniti:

Primjer 10

Provjerite jesu li sljedeći prostorni vektori kolinearni:
A)
b)

Otopina: Provjera se temelji na jednoj od izjava u ovoj lekciji: ako su vektori kolinearni, tada je njihov vektorski produkt jednak nuli (nulti vektor): .

a) Pronađite vektorski produkt:

Dakle, vektori nisu kolinearni.

b) Pronađite vektorski produkt:

Odgovor: a) nije kolinearan, b)

Ovdje su možda sve osnovne informacije o vektorskom produktu vektora.

Ovaj odjeljak neće biti velik, jer postoji nekoliko problema u kojima se koristi mješoviti umnožak vektora. Zapravo, sve će ovisiti o definiciji, geometrijskom značenju i nekoliko radnih formula.

Mješoviti produkt vektora je proizvod tri vektori:

Pa su se poredali kao vlak i jedva čekaju da ih se identificira.

Prvo, opet, definicija i slika:

Definicija: Mješoviti rad nekoplanarni vektori, uzeti ovim redom, nazvao volumen paralelopipeda, izgrađen na tim vektorima, opremljen znakom “+” ako je baza desna, i znakom “–” ako je baza lijevo.

Napravimo crtež. Nama nevidljive linije nacrtane su isprekidanim linijama:

Uronimo u definiciju:

2) Uzimaju se vektori određenim redoslijedom, odnosno preuređivanje vektora u umnošku, kao što pretpostavljate, ne događa se bez posljedica.

3) Prije nego što komentiram geometrijsko značenje, primijetit ću očitu činjenicu: mješoviti umnožak vektora je BROJ: . U obrazovnoj literaturi dizajn može biti malo drugačiji; ja sam navikao označavati mješoviti proizvod sa , a rezultat izračuna slovom "pe".

Po definiciji mješoviti umnožak je obujam paralelopipeda, izgrađen na vektorima (figura je nacrtana crvenim vektorima i crnim linijama). To jest, broj je jednak volumenu danog paralelopipeda.

Bilješka : Crtež je shematski.

4) Nemojmo opet brinuti o konceptu orijentacije osnove i prostora. Značenje završnog dijela je da se glasnoći može dodati znak minus. Jednostavnim riječima, mješoviti umnožak može biti negativan: .

Izravno iz definicije slijedi formula za izračunavanje volumena paralelopipeda izgrađenog na vektorima.

Definicija. Vektorski produkt vektora a i vektora b je vektor označen simbolom [α, b] (ili l x b), tako da je 1) duljina vektora [a, b] jednaka (p, gdje je y kut između vektora a i b (slika 31); vektor [a, b) je okomit na vektore a i b, tj. okomito na ravninu ovih vektora; 3) vektor [a, b] je usmjeren tako da se od kraja ovog vektora vidi najkraći zavoj od a do b u smjeru suprotnom od kazaljke na satu (slika 32). Riža. 32 Sl.31 Drugim riječima, vektori a, b i [a, b) tvore desni triplet vektora, tj. smješteni poput palca, kažiprsta i srednjeg prsta desne ruke. Ako su vektori a i b kolinearni, pretpostavit ćemo da je [a, b] = 0. Prema definiciji, duljina vektorskog umnoška brojčano je jednaka površini Sa paralelograma (sl. 33), konstruiranog na umnoženom vektori a i b kao stranice: 6.1 . Svojstva vektorskog umnoška 1. Vektorski umnožak jednak je nultom vektoru ako i samo ako je barem jedan od umnoženih vektora nula ili kada su ti vektori kolinearni (ako su vektori a i b kolinearni, tada je kut između njih jednak ili 0 ili 7r). Odredite površinu trokuta (slika 36). Jasno je da je površina b"d trokuta OAO jednaka polovici površine S paralelograma O AC B. Računajući vektorski produkt (a, b| vektora a = OA i b = ob, dobivamo, dakle, Napomena. Vektorski umnožak nije asocijativan, tj. jednakost ((a, b),c) = [a, |b,c)) nije istinita, na primjer, za a = ss j vrijedi §. 7. Mješoviti umnožak vektora Pomnožimo vektore a, b i c kao rezultat toga, pomnožimo ga skalarno s vektorom c: (k b ), c).Broj ([a, b], e) naziva se mješoviti umnožak vektora a, b i označava se simbolom (a, 1), e). u ovom slučaju nazivamo koplanarnim), tada je mješoviti umnožak ([a, b], c) = 0. To slijedi iz činjenice da je vektor [a, b| okomit na ravninu u kojoj leže vektori a i 1. ", a time i vektoru c. / Ako točke O, A, B, C ne leže u istoj ravnini (vektori a, b i c su nekoplanarni), konstruirat ćemo paralelopiped na bridovima OA, OB i OS (Sl. 38 a). Po definiciji vektorskog produkta imamo (a,b) = So c, gdje je So površina paralelograma OADB, a c je jedinični vektor okomit na vektore a i b i takav da je trostruki a , b, c je desnokretan, tj. vektori a, b i c nalaze se redom kao palac, kažiprst i srednji prst desne ruke (slika 38 b). Množenjem obje strane posljednje jednakosti s desne strane skalarno s vektorom c, dobivamo da je vektorski umnožak vektora zadan koordinatama. Mješoviti rad. Broj pc c jednak je visini h konstruiranog paralelopipeda, uzetom sa predznakom “+” ako je kut između vektora c i c oštar (trostruki a, b, c - desno), a sa “-” znak ako je kut tup (trostruki a, b, c - lijevo), tako da je dakle mješoviti umnožak vektora a, b i c jednak volumenu V paralelopipeda izgrađenog na tim vektorima kao na bridovima, ako trojka a, b, c je desno, a -V, ako je trojka a , b, c - lijevo. Na temelju geometrijskog značenja mješovitog umnoška možemo zaključiti da ćemo množenjem istih vektora a, b i c bilo kojim drugim redoslijedom uvijek dobiti ili +7 ili -K. Oznaka proizvođača Sl. 38 referenca ovisit će samo o tome kakvu trojku tvore umnoženi vektori - desnu ili lijevu. Ako vektori a, b, c tvore desnu trojku, tada će trojke b, c, a i c, a, b također biti desnokretne. Istodobno, sve tri trojke b, a, c; a, c, b i c, b, a - lijevo. Dakle, (a,b, c) = (b,c, a) = (c,a,b) = -(b,a,c) = -(a,c,b) = -(c,b, A). Ponovno naglašavamo da je mješoviti umnožak vektora jednak nuli samo ako su umnoženi vektori a, b, c koplanarni: (a, b, c su koplanarni) 7.2. Mješoviti umnožak u koordinatama Neka su vektori a, b, c zadani svojim koordinatama u bazi i, j, k: a = (x\,y\,z]), b= (x2,y2>z2), c = (x3, uz, 23). Nađimo izraz za njihov mješoviti produkt (a, b, c). Imamo mješoviti umnožak vektora specificiranih njihovim koordinatama u bazi i, J, k, jednak determinanti trećeg reda, čiji su pravci sastavljeni od koordinata prvog, drugog i trećeg umnoženog vektora. Potreban i dovoljan uvjet koplanarnosti vektora a y\, Z|), b = (hʺ U2.22), s = (žz, z, 23) zapisat ćemo u obliku U| z, ag2 y2 -2 =0. Uz primjer. Provjeriti jesu li vektori „ = (7,4,6), b = (2, 1,1), c = (19, II, 17) komplanarni. Izračunajte visinu h paralelopipeda izgrađenog na vektorima a = 31 + 2j - 5k, b = i- j + 4knc = i-3j + k, ako je za bazu uzet paralelogram izgrađen na vektorima a i I. Odgovori

7.1. Definicija unakrsnog umnoška

Tri nekomplanarna vektora a, b i c, uzeta naznačenim redoslijedom, tvore desni trostruk ako se od kraja trećeg vektora c vidi najkraći zavoj od prvog vektora a do drugog vektora b biti u smjeru suprotnom od kazaljke na satu, a ljevoruki triplet ako je u smjeru kazaljke na satu (vidi sl. .16).

Vektorski produkt vektora a i vektora b naziva se vektor c, koji:

1. Okomito na vektore a i b, tj. c ^ a i c ^ b ;

2. Ima duljinu numerički jednaku površini paralelograma konstruiranog na vektorima a ib kao na stranama (vidi sl. 17), t.j.

3. Vektori a, b i c tvore desnu trojku.

Križni umnožak označava se a x b ili [a,b]. Sljedeći odnosi između jediničnih vektora izravno slijede iz definicije vektorskog produkta, j I k

(vidi sliku 18):
i x j = k, j x k = i, k x i = j. Dokažimo, na primjer, da

i xj =k. ^ 1) k ^ i, k

j ; 2) |k |=1, ali | i x j

| = |i | I|J | sin(90°)=1;

3) vektori i, j i

tvore desnu trojku (vidi sliku 16).

7.2. Svojstva križnog umnoška = -(1. Pri preslagivanju faktora vektorski produkt mijenja predznak, tj.).

i xb =(b xa) (vidi sliku 19).

Vektori a xb i b xa su kolinearni, imaju iste module (površina paralelograma ostaje nepromijenjena), ali su suprotno usmjereni (trojke a, b, a xb i a, b, b x a suprotne orijentacije). Stoga axb b xa b 2. Vektorski produkt ima svojstvo kombiniranja u odnosu na skalarni faktor, tj. l ​​(a xb) = (l a) x b = a x (l b). b Neka je l >0. Vektor l (a xb) je okomit na vektore a i b. Vektor ( axb l axb sjekira axb b xa b također je okomit na vektore a i

(vektori a, axb ali leže u istoj ravnini). To znači da vektori axb(a xb) i ( axb<0.

kolinearni. Očito je da im se smjerovi poklapaju. Imaju istu dužinu: b su kolinearni ako i samo ako je njihov vektorski produkt jednak nultom vektoru, tj. a ||b<=>i xb =0.

Konkretno, i *i =j *j =k *k =0 .

4. Vektorski produkt ima svojstvo distribucije:

(a+b) xc = a xc + b xs.

Prihvatit ćemo bez dokaza.

7.3. Izražavanje umnoška preko koordinata

Koristit ćemo tablicu unakrsnog produkta vektora i, Sljedeći odnosi između jediničnih vektora izravno slijede iz definicije vektorskog produkta, i k:

ako se smjer najkraćeg puta od prvog vektora do drugog poklapa sa smjerom strelice, tada je umnožak jednak trećem vektoru; ako se ne poklapa, treći vektor se uzima s predznakom minus.

Neka su dana dva vektora a =a x i +a y Sljedeći odnosi između jediničnih vektora izravno slijede iz definicije vektorskog produkta,+a z I i b =b x ja+b g Sljedeći odnosi između jediničnih vektora izravno slijede iz definicije vektorskog produkta,+b z I. Nađimo vektorski umnožak ovih vektora množenjem kao polinoma (prema svojstvima vektorskog umnoška):

Dobivena formula može se napisati još kraće:

budući da desna strana jednakosti (7.1) odgovara proširenju determinante trećeg reda u smislu elemenata prvog reda. Jednakost (7.2) je lako zapamtiti.

7.4. Neke primjene križnog umnoška

Utvrđivanje kolinearnosti vektora

Određivanje površine paralelograma i trokuta

Prema definiciji vektorskog produkta vektora A i b |a xb | =|a | * |b |sin g, tj. S parova = |a x b |. I, prema tome, D S =1/2|a x b |.

Određivanje momenta sile oko točke

Neka na točku A djeluje sila F = AB i neka OKO- neka točka u prostoru (vidi sliku 20).

Iz fizike je poznato da moment sile F u odnosu na točku OKO nazvan vektor M, koji prolazi točkom OKO I:

1) okomito na ravninu koja prolazi kroz točke O, A, B;

2) brojčano jednak umnošku sile po kraku

3) tvori desnu trojku s vektorima OA i A B.

Stoga je M = OA x F.

Određivanje linearne brzine rotacije

Ubrzati v točka M krutog tijela koje rotira kutnom brzinom w oko fiksne osi, određuje se Eulerovom formulom v =w xr, gdje je r =OM, gdje je O neka fiksna točka osi (vidi sliku 21).