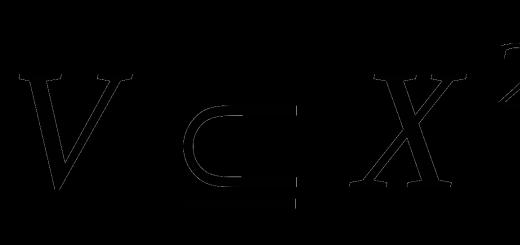Федеральное Государственное образовательное учреждение высшего профессионального образования

«Мордовский государственный педагогический институт имени М.Е. Евсевьева»

Физико-математический факультет

Реферат

по теме:

«Теория графов »

Выполнила: студентка

группы МДМ-109

Добрынкина О.А.

Проверила: Лапина И.Э.

Саранск 2014

Введение………………………………………………………………………. 3

1. Основные понятия теории графов………………………………………… 4

2. Примеры графов……………………………………………………………. 8

3. Эйлеровы графы…………………………………………………………… 13

4. Примеры приложений теории графов……………………………………. 16

5. Задача о кратчайшем пути………………………………………………… 18

6. Алгоритм нахождения максимального потока………………………….. 27

Заключение…………………………………………………………………… 38

Список литературы…………………………………………………………… 39

Введение

В последнее время наблюдается неуклонное вторжение математических методов в различные отрасли науки и техники. Процесс математизации затронул и экономическую науку.

Понятие графа, само по себе очень простое, оказалось весьма плодотворным в науке и часто употребляемым. Теория графов изучает графы как абстрактные математические образования, независимо от их конкретных истолкований, а полученные общие результаты затем прилагаются к самым различным дисциплинам.

Термин «граф» приобрел право гражданства и вошел в математический язык в 1936 г., после выхода в свет монографии Кёнига, в которой впервые графы изучаются как самостоятельные математические объекты независимо от их содержания.

Изучение графов актуально и на сегодняшний день. Найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут – все это примеры из нашей повседневной жизни. Эти и многие другие задачи могут быть решены при помощи графов.

В данной работе излагается ряд основных понятий, так же приведены примеры приложений теории графов и рассмотрены два подхода к решению экономических задач на основе теории графов.

1. Основные понятия теории графов

Граф – система, которая интуитивно может быть рассмотрена как множество кружков и множество соединяющих их линий (рис. 1).

Кружки называются вершинами графа, линии со стрелками – дугами, без стрелок – ребрами. Граф, в котором направление линий не выделяется (все линии являются ребрами), называется неориентированным (рис. 1, А); граф, в котором направление линий принципиально (линии являются дугами) называется ориентированным (рис. 1, Б).

Опр. 1. Задано конечное множество X , состоящее из n элементов (X = {1, 2,…, n }), называемых вершинами графа, и подмножество V декартова произведения X ×X, то есть
, называемое множеством дуг, тогда ориентированным графом G называется совокупность (X, V).

Опр. 2. Неориентированным графом называется совокупность множества X и множества неупорядоченных пар элементов, каждый из которых принадлежит множеству X.

Дугу между вершинами i и j,
, будем обозначать (i, j). Число дуг графа будем обозначать m (V = (
)).

Опр. 3. Подграфом называется часть графа, образованная подмножеством вершин вместе со всеми ребрами (дугами), соединяющими вершины из этого множества. Если из графа удалить часть ребер (дуг), то получим частичный граф.

Опр. 4. Две вершины называются смежными, если они соединены ребром (дугой). Смежные вершины называются граничными вершинами соответствующего ребра (дуги), а это ребро (дуга) – инцидентным соответствующим вершинам.

Опр.5. Путем называется последовательность дуг (в ориентированном графе), такая, что конец одной дуги является началом другой дуги.

Опр. 5.1. Простой путь – путь, в котором ни одна дуга не встречается дважды.

Опр. 5.2. Элементарный путь – путь, в котором ни одна вершина не встречается дважды.

Опр. 5.3. Контур – путь, у которого конечная вершина совпадает с начальной вершиной.

Опр. 5.4 Длиной пути (контура) называется число дуг пути (или сумма длин его дуг, если последние заданы).

Опр.6. Граф, для которого из (i, j) V следует (j, i) V называется симметрическим.

Опр. 7. Если из (i, j) V следует, что (j, i)
V, то соответствующий граф называется антисимметрическим.

Опр. 8.1. Цепью называется множество ребер (в неориентированном графе), которые можно расположить так, что конец (в этом расположении) одного ребра является началом другого.

Опр. 8.2. Цепь – последовательность смежных вершин.

Опр. 9. Замкнутая цепь называется циклом.

Опр. 10.1. Элементарная цепь (цикл, путь, контур), проходящая через все вершины графа называется гамильтоновой цепью (соответственно – циклом, путем, контуром).

Опр. 10.2. Простая цепь (цикл, путь, контур), содержащая все ребра (дуги) графа называется эйлеровой цепью (соответственно – циклом, путем, контуром).

Опр. 11. Если любые две вершины графа можно соединить цепью, то граф называется связным. Если граф не является связным, то его можно разбить на связные подграфы, называемые компонентами.

Опр. 12. Связностью графа называется минимальное число ребер, после удаления которых граф становится несвязным. Для ориентированных графов, если любые две вершины графа можно соединить путем, то граф называется сильно связным. Связный граф, в котором существует эйлеров цикл, называется эйлеровым графом.

Опр. 13. В неориентированном графе степенью вершины i называется число инцидентных ей ребер. Очевидно,
. Граф, степени всех вершин которого равны n – 1, называется полным. Граф, все степени вершин которого равны, называется однородным.

Опр. 14. Вершина, для которой не существует инцидентных ей ребер (= 0) называется изолированной. Вершина, для которой существует только одно инцидентное ей ребро ( = 1) называется висячей.

Опр. 15. Определим матрицу смежности графа как квадратную матрицу n ×n, элемент которой равен единице, если (i, j) V, и нулю, если (i, j)
V, i, jX. Для неориентированного графа матрица смежности всегда симметрическая.

Опр. 16. Определим матрицу инциденций для ребер графа как прямоугольную матрицу n×m, элемент которой равен единице, если вершина i инцидентна ребру j, и нулю в противном случае, i = 1, n, j = 1, m.

Опр. 17. Матрица инциденций для дуг графа – прямоугольная матрицу m x n, элемент rij которой равен плюс единице, если дуга исходит из вершины i, минус единице, если дуга заходит в вершину i, и нулю в остальных случаях, i = 1, n, j = 1, m

Опр. 18. Деревом называется связный граф без простых циклов, имеющий не менее двух вершин. Для дерева m = n – 1, а число висячих вершин равно
Легко показать, что в дереве любые две вершины связаны единственной цепью.

Опр. 19. Прадеревом называется ориентированное дерево, у которого одна из вершин, называемая корнем, не имеет заходящих дуг, а степени захода остальных вершин равны единице.

Опр. 20. Плоским (планарным) называется граф, который можно изобразить на плоскости так, что различным вершинам соответствуют различные кружки и никакие два ребра не имеют общих точек, отличных от их границ (не пересекаются). Для плоского графа существует понятие грани – части плоскости, ограниченной ребрами и не содержащей внутри себя ни вершин, ни ребер.

Опр. 21. Степенью грани называется число ее граничных ребер (висячие ребра считаются дважды).

Любому связному плоскому графу G можно поставить в соответствие двойственный ему связный плоский граф G*, определяемый следующим образом: каждой грани графа G соответствует вершина графа G*, каждому ребру V графа G, являющемуся граничным для граней z1 и z2, соответствует ребро V* графа G*, соединяющее соответствующие граням z1 и z2 вершины.

2. Примеры графов

Вполне несвязные графы . Граф, у которого множество ребер пусто, называется вполне несвязным (или пустым) графом. Будем обозначать вполне несвязный граф с п вершинами через N n ; N 4 показан на рис. 1. Заметим, что у вполне несвязного графа все вершины изолированы. Вполне несвязные графы не представляют особого интереса.

Полные графы . Простой граф, в котором любые две вершины смежны, называется полным графом. Полный граф с n вершинами обычно обозначается через . Графы и изображены на рис. 2 и 3. имеет ровно n (n – 1)/2 ребер.

Регулярные графы . Граф, у которого все вершины имеют одну и ту же степень, называется регулярным графом. Если степень каждой вершины равна r , то граф называется регулярным степени r . Регулярные графы степени 3, называемые также кубическими (или трехвалентными) графами (см., например, рис. 2 и 4). Другим известным примером кубического графа является так называемый граф Петерсена, показанный на рис. 5. Отметим, что каждый вполне несвязный граф является регулярным степени 0, а каждый полный граф К n – регулярным степени n – 1.

Платоновы графы . Среди регулярных графов особенно интересны так называемые Платоновы графы – графы образованные вершинами и ребрами пяти правильных многогранников – платоновых тел: тетраэдра, куба, октаэдра, додекаэдра и икосаэдра. Граф соответствует тетраэдру (рис. 2); графы, соответствующие кубу и октаэдру, показаны на рис. 5 и 6;

Двудольные графы . Допустим, что множество вершин графа можно разбить на два непересекающихся подмножества V 1 и V 2 так, что каждое ребро в G соединяет какую-нибудь вершину из V 1 с какой-либо вершиной из V 2 (рис. 7);

тогда G называется двудольным графом. Такие графы иногда обозначают G (V 1, V 2), если хотят выделить два указанных подмножества. Двудольный граф можно определить и по-другому – в терминах раскраски его вершин двумя цветами, скажем красным и синим. При этом граф называется двудольным, если каждую его вершину можно окрасить красным или синим цветом так, чтобы любое ребро имело один конец красный, а другой – синий. Следует подчеркнуть, что в двудольном графе совсем не обязательно каждая вершина из V 1 соединена с каждой вершиной из V 2 ; если же это так и если при этом граф G простой, то он называется полным двудольным графом и обычно обозначается

где m , n – число вершин соответственно в V 1 и V 2 . Например, на рис. 8 изображен граф K 4 , 3 . Заметим, что граф
имеет ровно m + n вершин и mn ребер. Полный двудольный граф вида
называется звездным графом; на рис. 9 изображен звездный граф
.

Связные графы . Граф связный, если его нельзя представить в виде объединения двух графов, и несвязный в противном случае. Очевидно, что всякий несвязный граф G можно представить в виде объединения конечного числа связных графов – каждый из таких связных графов называется компонентой (связности) графа G . (На рис. 10 изображен граф с тремя компонентами.) Доказательство некоторых утверждений для произвольных графов часто бывает удобно сначала провести для связных графов, а затем применить их к каждой компоненте в отдельности.

Циклические графы и колеса . Связный регулярный граф степени 2 называется циклическим графом (или циклом); циклический граф. с п вершинами обозначается через С n . Соединение графов и
(п ≥ 3) называется колесом с п вершинами и обозначается W n . На рис. 11 изображены С 6 и W 6 ; граф W 4 уже появлялся на рис. 2.

3. Эйлеровы графы

Связный граф G называется эйлеровым, если существует замкнутая цепь, проходящая через каждое его ребро; такая цепь называется эйлеровой цепью. Отметим, что в этом определении требуется, чтобы каждое ребро проходилось только один раз. Если снять ограничение на замкнутость цепи, то граф называется полуэйлеровым; при этом каждый эйлеров граф будет полуэйлеровым. На рис. 13,14,15 изображены соответственно не эйлеров, полуэилеров и эйлеров графы.

Название «эйлеров» возникло в связи с тем, что Эйлер первым решил знаменитую задачу о кенигсбергских мостах, в которой нужно было узнать, имеет ли граф, изображенный на рис. 15, эйлерову цепь (не имеет). Сразу же возникает вопрос: можно ли найти необходимые и достаточные условия для того, чтобы граф был эйлеровым

Докажем простую лемму.

Лемма 1. Если степень каждой вершины графа G не меньше двух, то G содержит цикл.

Доказательство. Если в графе G имеются петли или кратные ребра, то утверждение очевидно; поэтому предположим, что G является простым графом. Пусть v – произвольная вершина графа G ; построим по индукции маршрут , выбирая вершину v 1 смежной вершине v , а для i ≥1 – выбирая v i +1 смежной v i и отличной от v i -1 (существование такой вершины v i +1 гарантировано условием леммы). Так как G имеет конечное число вершин, то в конце концов мы придем к вершине, которая уже была выбрана раньше. Предположим, что v k – первая такая вершина; тогда часть маршрута, лежащая между двумя вхождениями v h , и является требуемым циклом.

Теорема 1. Связный граф G является эйлеровым тогда и только тогда, когда каждая вершина в G имеет четную степень.

Доказательство.
Предположим, что Р является эйлеровой цепью в графе G . Тогда при всяком прохождении цепи Р через любую из вершин графа степень этой вершины увеличивается на два. А так как каждое ребро встречается в Р ровно один раз, то каждая вершина должна иметь четную степень.

Проведем доказательство индукцией по числу ребер в G . В силу связности G , степень каждой вершины не меньше двух, а отсюда, по предыдущей лемме, заключаем, что граф G содержит цикл С. Если С проходит через каждое ребро графа G , то доказательство завершено; если нет, то, удаляя из G ребра, принадлежащие циклу С, получим новый (быть может, и несвязный) граф Н. Число ребер в Н меньше, чем в G , и любая вершина в Н по-прежнему имеет четную степень. Согласно индуктивному предположению, в каждой компоненте графа Н существует эйлерова цепь. В силу связности графа G , каждая компонента в Н имеет по крайней мере одну общую вершину с циклом С, поэтому искомую эйлерову цепь графа G можно получить так: идем по ребрам цикла С до тех пор, пока не встретим неизолированную вершину графа Н, затем следуем по эйлеровой цепи той компоненты в Н, которая содержит указанную вершину; далее продолжаем путь по ребрам цикла С, пока не встретим вершину, принадлежащую другой компоненте графа Н, и т.д.; заканчивается процесс тогда, когда мы попадаем обратно в начальную вершину (рис. 17).

Следствие 1. Связный граф является эйлеровым тогда и только тогда, когда семейство его ребер можно разбить на непересекающиеся циклы.

Следствие 2. Связный граф является полуэйлеровым тогда и только тогда, когда в нем не более двух вершин имеют нечетные степени.

4. Примеры приложений теории графов

1. «Транспортные» задачи, в которых вершинами графа являются пункты, а ребрами – дороги (автомобильные, железные и др.) и / или другие транспортные (например, авиационные) маршруты. Другой пример – сети снабжения (энергоснабжения, газоснабжения, снабжения товарами и т.д.), в которых вершинами являются пункты производства и потребления, а ребрами – возможные маршруты перемещения (линии электропередач, газопроводы, дороги и т.д.). Соответствующий класс задач оптимизации потоков грузов, размещения пунктов производства и потребления и т.д., иногда называется задачами обеспечения или задачами о размещении. Их подклассом являются задачи о грузоперевозках.

2. «Технологические задачи», в которых вершины отражают производственные элементы (заводы, цеха, станки и т.д.), а дуги потоки сырья, материалов и продукции между ними, заключаются в определении оптимальной загрузки производственных элементов и обеспечивающих эту загрузку потоков.

3. Обменные схемы, являющиеся моделями таких явлений как бартер, взаимозачеты и т.д. Вершины графа при этом описывают участников обменной схемы (цепочки), а дуги – потоки материальных и финансовых ресурсов между ними. Задача заключается в определении цепочки обменов, оптимальной с точки зрения, например, организатора обмена и согласованной с интересами участников цепочки и существующими ограничениями

4. Управление проектами. (Управление проектами – раздел теории управления, изучающий методы и механизмы управления изменениями (проектом называется целенаправленное изменение некоторой системы, осуществляемое в рамках ограничений на время и используемые ресурсы; характерной чертой любого проекта является его уникальность, то есть нерегулярность соответствующих изменений.)). С точки зрения теории графов проект – совокупность операций и зависимостей между ними. Хрестоматийным примером является проект строительства некоторого объекта. Совокупность моделей и методов, использующих язык и результаты теории графов и ориентированных на решение задач управления проектами, получила название календарно-сетевого планирования и управления (КСПУ). В рамках КСПУ решаются задачи определения последовательности выполнения операций и распределения ресурсов между ними, оптимальных с точки зрения тех или иных критериев (времени проекта, затрат, и др.).

5. Модели коллективов и групп, используемые в социологии, основываются на представлении людей или их групп в виде вершин, а отношений между ними (например, отношений знакомства, доверия, симпатии и т.д.) – в виде ребер или дуг. В рамках подобного описания решаются задачи исследования структуры социальных групп, их сравнения, определения агрегированных показателей, отражающих степень напряженности, согласованности, взаимодействия и др.

6. Модели организационных структур, в которых вершинами являются элементы организационной системы, а ребрами или дугами – связи (информационные, управляющие, технологические и др.) между ними.

5. Задача о кратчайшем пути

Пример 1. Задача о волке, козе и капусте. Коза, капуста и волк находятся на берегу реки; перевозчику надо переправить их через реку, но его лодка так мала, что он может взять с собой не более одною из этих трех «пассажиров». По очевидным причинам нельзя оставлять без надзора волка с козой, а козу с капустой. Как должен поступить перевозчик?

Эта широко известная задача легко решается в уме благодаря малому числу вариантов, подлежащих рассмотрению, тем не менее перед нами типичный пример задачи, о нахождении кратчайшего пути: чертится граф изображенный на рис 1 и ищется путь, ведущий из положения а (когда коза К, капуста Кап, волк В и перевозчик П находятся на правом берегу) в положение b (когда все переправлены на левый берег), искомый путь показан на рисунке жирными линиями.

В более общем случае необходим систематический алгоритм, изложим несколько методов.

Задача о кратчайшем пути

Пусть задана сеть из n + 1 вершины, то есть ориентированный граф, в котором выделены две вершины – вход (нулевая вершина) и выход (вершина с номером n). Для каждой дуги заданы числа, называемые длинами дуг. Длиной пути (контура) называется сумма длин входящих в него дуг

(если длины дуг не заданы, то длина пути (контура) определяется как число входящих в него дуг). Задача заключается в поиске кратчайшего пути (пути минимальной длины) от входа до выхода сети.

Для существования кратчайшего пути необходимо и достаточно отсутствия в сети контуров отрицательной длины.

Предположим, что в сети нет контуров. Тогда всегда можно пронумеровать вершины таким образом, что для любой дуги (i, j) имеет место j > i. Такая нумерация называется правильной. Легко показать, что в сети без контуров всегда существует правильная нумерация.

Обозначим – длину дуги (i; j). Кратчайший путь в сети, имеющей правильную нумерацию, определяется следующим алгоритмом.

Алгоритм 1.

;

Шаг k: помечаем вершину k индексом
i

Индекс выхода будет равен длине кратчайшего пути. (Алгоритм 1 для задач динамического программирования отражает принцип оптимальности Беллмана: если ищется кратчайший путь между двумя точками, то длина пути между любыми двумя точками кратчайшего пути также должна быть минимальна.) На рисунке 2 приведен пример применения алгоритма 1 для определения кратчайшего пути (числа у дуг равны длинам дуг, индексы вершин помещены в квадратные скобки, кратчайший путь выделен двойными линиями).

Когда индексы (называемые в некоторых задачах потенциалами вершин) установятся, кратчайший путь определяется методом обратного хода от выхода к входу, то есть кратчайшим является путь
, такой, что
и т.д.

Следующий алгоритм дает возможность определять кратчайший путь в общем случае (то есть при произвольной нумерации вершин).

Алгоритм 2 (алгоритм Форда).

Шаг 0: Помечаем нулевую вершину индексом
, все остальные вершины индексами
, i = 1, n;

Шаг k: Рассматриваем все дуги. Если для дуги (i; j)
>, то вычисляем новое значение
;

Индексы устанавливаются за конечное число шагов. Обозначим
- установившиеся значения индексов, которые обладают следующим свойством: величина равна длине кратчайшего пути из нулевой вершины в вершину i. Кратчайший путь из вершины 0 в вершину i определяется методом обратного хода.

Если длины всех дуг неотрицательны, то для поиска кратчайшего пути применим следующий алгоритм.

Алгоритм 3.

Шаг 0: Помечаем нулевую вершину индексом
;

Шаг k: Пусть уже помечено некоторое множество вершин. Обозначим Q – множество непомеченных вершин, смежных с помеченными. Для каждой вершины
вычисляем величину
где минимум берется по всем помеченным вершинам i, смежным с вершиной k. Помечаем вершину k, для которой величина минимальна, индексом
.

Подобную процедуру повторяем до тех пор, пока не будет помечена вершина n. Длина кратчайшего пути равна , а сам кратчайший путь определяется так, как это было описано выше.

Аналогично задаче о кратчайшем пути формулируется и решается задача о максимальном (длиннейшем) пути – достаточно изменить знаки дуг на противоположные и решить задачу о кратчайшем пути. Для существования решения задачи о максимальном пути необходимо и достаточно отсутствия контуров положительной длины.

В задаче поиска пути максимальной надежности длины дуг интерпретируются, например, как вероятности того, что существует связь между соответствующими двумя пунктами. Заменяя длины дуг их логарифмами, взятыми с обратными знаками, получаем, что путь максимальной надежности в исходном графе будет соответствовать кратчайшему пути в новом графе.

Пример 1.

Рис. 3. Исходные данные к задаче о кратчайшем пути.

Ситуацию можно описать не только ориентированным графом, но и таблицей (табл. 1).

Табл.1. Исходные данные к задаче о кратчайшем пути

Начало дуги

Конец дуги

Время в пути

Спрашивается в задаче: как кратчайшим путем попасть из вершины 1 в вершину 4?

Решение. Введем обозначение: С (Т) – длина кратчайшего пути из вершины 1 в вершину Т. (Поскольку любой путь, который надо рассмотреть, состоит из дуг, а дуг конечное число, и каждая входит не более одного раза, то претендентов на кратчайший путь конечное число, и минимум из конечного числа элементов всегда достигается.) Рассматриваемая задача состоит в вычислении С (4) и указании пути, на котором этот минимум достигается.

Для исходных данных, представленных на рис. 3 и в табл. 1, в вершину 3 входит только одна стрелка, как раз из вершины 1, и около этой стрелки стоит ее длина, равная 1, поэтому С(3)=1. Кроме того, очевидно, что С(1)=0.

В вершину 4 можно попасть либо из вершины 2, пройдя путь, равный 4, либо из вершины 5, пройдя путь, равный 5. Поэтому справедливо соотношение С(4) = min {С(2) + 4; С(5) + 5}.

Таким образом, проведена реструктуризация задачи – нахождение С(4) сведено к нахождению С(2) и С(5).

В вершину 5 можно попасть либо из вершины 3, пройдя путь, равный 2, либо из вершины 6, пройдя путь, равный 3. Поэтому справедливо соотношение С(5) = min {С(3) + 2; С(6) + 3}.

Мы знаем, что С(3) = 1. Поэтому С(5) = min {3; С(6) + 3}.

Поскольку очевидно, что С(6) – положительное число, то из последнего соотношения вытекает, что С(5) = 3.

В вершину 2 можно попасть либо из вершины 1, пройдя путь, равный 7, либо из вершины 3, пройдя путь, равный 5, либо из вершины 5, пройдя путь, равный 2. Поэтому справедливо соотношение С(2) = min {С(1) + 7; С(3) + 5; С(5) + 2}.

Нам известно, что С(1) = 0, С(3) = 1, С(5) = 3. Поэтому С(2) = min {0 + 7; 1 + 5; 3 + 2} = 5.

Теперь мы можем найти С(4): С(4) = min {С(2) + 4; С(5) + 5} = min {5 + 4; 3 + 5} = 8.

Таким образом, длина кратчайшего пути равна 8. Из последнего соотношения ясно, что в вершину 4 надо идти через вершину 5. Возвращаясь к вычислению С(5), видим, что в вершину 5 надо идти через вершину 3. А в вершину 3 можно попасть только из вершины 1. Итак, кратчайший путь таков: 1 → 3 → 5 → 4.

Задача о кратчайшем пути для конкретных исходных данных (рис. 3и табл. 1) полностью решена.

Пример 2.

Найти кратчайший путь (длина пути) из Академгородка (остановка Цветной проезд) до железнодорожного вокзала.

Остановки:

цветной проезд

дом быта

3,3"- институт ядерной физики

4 Баня №22

5 Речной вокзал

6 – Сеятель

7 – кафе «Огонек»

8 – Мост

9 – Главный Вокзал

Найти кратчайший путь из вершины 1 в вершины 9.

Исходные данные:

Рис. 4

Табл. 2

Начало дуги

Конец дуги

Длина пути (км.)

3,06

10,9

26,78

21,57

4,26

4,35

2,55

Решение: С (Т) – длина кратчайшего пути из вершины 1 в вершину Т. Нам необходимо найти С(9).

С(1)=0, С(2)=3 (в вершину 2 входит только одна стрелка, ее длина равна 3).

В вершину 9 можно попасть из вершины 5, пройдя путь 4,35, из вершины 6, пройдя путь 25 и из вершины 8, пройдя путь 2,55.

Следовательно, С(9) = min {С(5) + 4,35; С(6) + 25; С(8) + 2,55}

Таким образом необходимо найти С(5), С(6), С(8).

В вершину 5 можно попасть из вершины 1, пройдя путь 26,78, либо из вершины 7, пройдя путь 19

С(5) = min {С(1) + 26,78; С(7) + 19}

Необходимо найти С(7). В вершину 7 можно попасть из вершины 3, пройдя путь 7,6 и из 3" пройдя 7,6.

С(7) = min {С(3) + 7,6; С(3") + 7,6}= min {1,7+7,6; 3,06+7,6}=9,3

С(5) = min {26,78; 9,3+ 19}=26,78

В вершину 6 можно попасть из вершины 2, пройдя путь равный 0,5

С(6)=С(2)+0,5=3+0,5=3,5

В вершину 8 можно попасть из вершины 4, пройдя путь 21,57 и из вершины 5, пройдя путь 4,62.

С(8) = min {С(4) + 21,57; С(5) + 4,26}

С(4)=10,9 (из условия).

С(8) = min {10,09+ 21,57; 26,78 + 4,26}=31,4

Следовательно

С(9)= min {26,78+4,35; 3,5+25; 31,4+2,55}= min {31,13; 28,5; 33,95}=28,5

Таким образом, длина кратчайшего пути равна 28,5 км.

Кратчайший путь: 1 → 2 → 6 → 9.

6. Алгоритм нахождения максимального потока

Идея этого алгоритма состоит в поиске сквозных путей с положительными потоками от источника к стоку.

Рассмотрим ребро (i , j ) с (начальной) пропускной способностью
. В процессе выполнения алгоритма части этих пропускных способностей «забираются» потоками, проходящими через данное ребро, в результате каждое ребро будет иметь остаточную пропускную способность. Запись
- остаточная пропускная способность. Сеть в которой все ребра имеют остаточную пропускную способность, назовем остаточной.

Для произвольного узла j , получающего поток из узла i , определим метку
, где - величина потока, протекающего от j узла к узлу i . Чтобы найти максимальный поток, выполняем следующие действия.

Этап 1.

Для всех ребер положим остаточную пропускную способность равной первоначальной пропускной способности, т.е. приравняем
=
. Назначим
и пометим узел 1 меткой. Полагаем i =1.

Этап 2.

- множество узлов j , в которые можно перейти из узла I по ребру с положительной остаточной пропускной способностью >0 для всех j . Если
, выполняем 3 этап, в противном случае переходим к 4.

Этап 3.

В находим узел k , такой, что
. Положим
и пометим узел k меткой
. Если k =n , сквозной путь найден, и переходим к 5 этапу, в противном случае полагаем i =k и возвращаемся к 2 этапу.

Этап 4.

Откат назад. Если i =1, сквозной путь не возможен, и переходим к 6. Если
, находим помеченный узел r , непосредственно предшествующий узлу i , и удаляем его из множества узлов, смежных с узлом r . Полагаем i =r и возвращаемся ко 2 этапу.

Этап 5.

Определение остаточной сети
. Обозначим через множество узлов, через которые проходит p й найденный сквозной путь от узла источника (узел 1) до узла стока (узел n ).тогда максимальный поток, проходящий по этому пути

Остаточные пропускные способности ребер, составляющих сквозной путь, уменьшаются на величину в направлении движения потока и увеличиваются на эту же величину в противоположном направлении.

Т.о. для ребра (i , j ), входящего в сквозной путь, текущие остаточные пропускные способности изменяются:

1)
, если поток идет от узла i к j ,

2)
, если поток идет от узла j к i .

Этап 6.

Решение.

а) при m найденных сквозных путях максимальный поток выражается

б) Имея значения начальных
и конечных
пропускных способностей ребра (i , j ), можно вычислить оптимальный поток через это ребро следующим образом. Положим . Если >0, поток, проходящий через ребро (i , j ) равен . Если >0, тогда поток равен . (случай, когда одновременно >0 и >0, невозможен).

Пример 1. Найти максимальный поток в сети рис. 1

Итерация 1.
=

1)
и помечаем узел 1 меткой
. i =1

2)

3) k =3, так как . Назначаем
и помечаем узел 3 меткой
. i =3 и возвращаемся к 2)

4)

5) k =5 и . Помечаем узел 5 меткой
. Получаем сквозной путь.

6) сквозной путь определяем по меткам, начиная с узла 5 и заканчивая узлом 1: .
:

Итерация 2.

1)
и помечаем узел 1 меткой
. i =1

2)

3) k =2, и помечаем узел 2 меткой
. i =2 и возвращаемся к 2)

2")

3") k =3 и
. Помечаем узел 3 меткой
. i =3 и возвращаемся к 2)

2»)
(
, поэтому узел 5 не включается в

3») k =4,
и помечаем узел 4 меткой
. i =4 и возвращаемся к 2)

2""")
(так как узлы 1 и 3 помечены, они не включаются в )

3""") k =5 и
. Помечаем узел 5 меткой
. Получен сквозной путь. Переходим к 5)

5)
и . Вычисляем остаточные пропускные способности вдоль пути :

Итерация 3.

1)
и помечаем узел 1 меткой
. i =1

2)

3) k =2,
и помечаем узел 2 меткой
. i =2 и возвращаемся к 2)

2")

Рис. 2. Исходные данные к примеру 2

Исходные данные о транспортной системе, например, внутризаводской, приведенные на рис. 2, можно также задать таблицей (табл. 2).

Табл.2. Исходные данные к задаче о максимальном потоке

Пункт отправления

Пункт назначения

Пропускная способность

Очевидно, максимальная пропускная способность транспортной системы не превышает 6, поскольку не более 6 единиц грузов можно направить из начального пункта 0, а именно, 2 единицы в пункт 1, 3 единицы в пункт 2 и 1 единицу в пункт 3. Далее надо добиться, чтобы все 6 вышедших из пункта 0 единиц груза достигли конечного пункта 4. Очевидно, 2 единицы груза, пришедшие в пункт 1, можно непосредственно направить в пункт 4. Пришедшие в пункт 2 грузы придется разделить: 2 единицы сразу направить в пункт 4, а 1 единицу – в промежуточный пункт 3 (из-за ограниченной пропускной способности участка между пунктами 2 и 4). В пункт 3 доставлены такие грузы: 1 единица из пункта 0 и 1 единица из пункта 3. Их направляем в пункт 4. Итак, максимальная пропускная способность рассматриваемой транспортной системы – 6 единиц груза. При этом не используются внутренние участки (ветки) между пунктами 1 и 2, а также между пунктами 1 и 3. Не догружена ветка между пунктами 1 и 4 – по ней направлены 2 единицы груза при пропускной способности в 3 единицы. Решение можно представить в виде таблицы (табл. 3)

Табл.3. Решение задачи о максимальном потоке

Пункт отправления

Пункт назначения

План перевозок

Пропускная способность

Задача линейного программирования при максимизации потока. Дадим формулировку задачи о максимальном потоке в терминах линейного программирования. Пусть Х KM - объем перевозок из пункта К в пункт М. Согласно рис. 2 К = 0,1,2,3, М = 1,2,3,4, причем перевозки возможны лишь в пункт с большим номером. Значит, всего имеется 9 переменных Х KM, а именно, Х 01, Х 02, Х 03, Х 12, Х 13, Х 14, Х 23, Х 24, Х 34. Задача линейного программирования, нацеленная на максимизацию потока, имеет вид:

F → max,

Х 01 + Х 02 + Х 03 = F (0)

– Х 01 + Х 12 + Х 13 + Х 14 = 0 (1)

– Х 02 - Х 12 + Х 23 + Х 24 = 0 (2)

– Х 03 - Х 13 - Х 23 + Х 34 = 0 (3)

– Х 14 - Х 24 - Х 34 = – F (4)

Х 01 ≤ 2

Х 02 ≤ 3

Х 03 ≤ 1

Х 12 ≤ 4

Х 13 ≤ 1

Х 14 ≤ 3

Х 23 ≤ 1

Х 24 ≤ 2

Х 34 ≤ 2

Х КМ ≥ 0, К, М = 0, 1, 2, 3, 4

F ≥ 0.

Здесь F – целевая функция, условие (0) описывает вхождение грузов в транспортную систему. Условия (1) – (3) задают балансовые соотношения для узлов 1- 3 системы. Другими словами, для каждого из внутренних узлов входящий поток грузов равен выходящему потоку, грузы не скапливаются внутри и системы и не «рождаются» в ней. Условие (4) – это условие «выхода» грузов из системы. Вместе с условием (0) оно составляет балансовое соотношение для системы в целом («вход» равен «выходу»). Следующие девять неравенств задают ограничения на пропускную способность отдельных «веток» транспортной системы. Затем указана неотрицательность объемов перевозок и целевой функции. Ясно, что последнее неравенство вытекает из вида целевой функции (соотношения (0) или (4)) и неотрицательности объемов перевозок. Однако последнее неравенство несет некоторую общую информацию – через систему может быть пропущен либо положительный объем грузов, либо нулевой (например, если внутри системы происходит движение по кругу), но не отрицательный (он не имеет экономического смысла, но формальная математическая модель об этом «не знает»).

Заключение

В данной работе мы рассмотрели необходимый минимум понятий, которые позволяют нам продолжить изучение теории графов. Ведь мы затронули лишь вершину огромного айсберга, разобрав пару подходов к решению экономических задач. Теория графов не ограничивается изучением каких-то отдельных явлений или процессов, она находит применение в самых разнообразных областях науки и техники.

Были рассмотрены алгоритмы решения задачи о кратчайшем пути и нахождения максимального потока, разобраны примеры. На их примере была показана значимость теории графов для оптимизации экономических задач.

Так же была составлен и решен пример о кратчайшем пути непосредственно, касающийся нашей повседневной жизни. Задача состояла в отыскании кратчайшего пути (длинны дороги в км.) от Академгородка (остановка Цветной проезд) до Вокзала Главного.

Список литературы

"Соросовский образовательный журнал" №11 1996 (ст. "Плоские графы");

«В помощь учителю математики», Йошкар-Ола, 1972 ст. "Изучение элементов теории графов"

Берж, К.С.Теория графов и ее применение./К. С. Берж.- М.: ИЛ, 2007.-178с.

Бурков, В.Н. Элементы теории графов./В. Н. Бурков. – М.: Просвещение,2010.-352с.

Гарднер, М. С"Математические досуги". / М. С. Гарднер.- М. :"Мир",2004.-347с.

Гарднер, М. С."Математические головоломки и развлечения"./ М С гарднер.-М. :"Мир",2005.-221с.

Зыков, А. А. Теория конечных графов./ А. А. Зыков.- Новосибирск: "Наука",2006.-257с.

Касаткин, В. Н. "Необычные задачи математики"./ В. Н. Касаткин.-Киев: "Радяньска школа", 2007.-232с.

Олехник, С. Н. "Старинные занимательные задачи"./ C .Н. Олехник.- М. "Наука",2008.-431с.

Оре, О. С."Графы и их применения"./О. С. Оре.- М.:"Мир", 2005-269с.

Реньи, А. Н."Трилогия о математике"./ А. Н. Реньи.- М.:"Мир",2010-198с.

Между элементами множества вершин и множества ребер определено отношение инцидентности. Говорят, что ребро е инцидентно вершинам v1, v2, если оно соединяет эти вершины и наоборот, каждая из вершин v1, v2 инцидентна ребру е.

Рассмотрим графическое представление графов таблица 1.

Таблица 1. Графическое представление графов

Многие результаты, полученные для простых графов, без труда модно перенести на более общие объекты, в которых две вершины могут быть соединены более чем одним ребром. Кроме того, часто бывает удобно снять ограничение, состоящее в том, что ребро должно соединять две различные вершины, и допустить существование петель. Получающийся при этом объект, в котором могут быть и кратные ребра и петли называется графом (псевдографом). Псевдограф без петель называется мультиграфом

Рассмотрим некоторые важные типы графов.

Определение. Граф, у которого множество ребер пусто, называется вполне несвязным (или пустым) графом. Вполне несвязный граф обозначают N

Заметим, что у вполне несвязного графа все вершины изолированы

Определение. Простой граф, в котором любые две вершины смежны, называется полным. Полный граф обозначают K

Заметим, что для полного графа выполняется равенство

где m - число ребер, n - число вершин графа.

Определение. Граф, у которого все вершины имеют одну и ту же локальную степень n, называется регулярным (или однородным) степени n.

Регулярные графы степени 3 называются кубическими (или трехвалентными).

Известным примером кубического графа является граф Петерсона

Среди регулярных графов особенно интересны так называемые платоновы графы - графы, образованные вершинами и ребрами пяти правильных многогранников - Платоновых тел: тетраэдра, куба, октаэдра, додекаэдра и икосаэдра.На рисунке 6 приведен граф, соответствующий кубу.

Определение. Допустим, что множество вершин графа G можно разбить на два непересекающихся подмножества V1 и V2 так, что каждое ребро в G соединяет какую-нибудь вершину из V1 с какой-нибудь вершиной из V2, тогда данный граф называется двудольным.

Двудольный граф можно определить и по-другому - в терминах раскраски его вершин двумя цветами, скажем красным и синим. При этом граф называется двудольным, если каждую его вершину можно окрасить красным или синим цветом так, чтобы каждое ребро имело один конец красный, а другой - синий.

Определение. Если в двудольном графе каждая вершина из V1 соединена с каждой вершиной из V2, то граф называется полным двудольным.

Заметим, что граф Кm. n имеет ровно m + n вершин и mn ребер.

Определение. Объединением графов

называется граф

Определение. Пересечением графов

называется граф

Определение. Соединением графов G1 и G2 является новый граф, у которого

а множеством ребер являются все ребра первого и второго графа и ребра, соединяющие между собой каждую вершину первого графа с первой вершиной второго графа.

Определение. Граф называется связным, если его нельзя представить в виде объединения двух графов, и несвязным в противном случае.

Очевидно, что всякий несвязный граф можно представить в виде объединения конечного числа связных графов - каждый из таких связных графов называется компонентой связности графа.

Определение. Связный регулярный граф степени 2 называется циклическим графом. Обозначается Сn .

Определение. Соединение графов N1 и Cn-1 (n3) называется колесом с n вершинами. Обозначается Wn (рисунок 10)

Определение. Дополнением простого графа G называется простой граф с множеством вершин V(G), в котором две вершины смежны тогда и только тогда, когда они не смежны в исходном графе.

Обозначение. Другими словами, дополнением графа является граф, содержащий все вершины исходного графа и только те ребра, которых не хватает исходному графу для того, чтобы он стал полным.

Определение. Подграфом графа G называется граф, все вершины и ребра которого содержатся среди вершин и ребер графа G. Подграф называется собственным, если он отличен от самого графа.

МУНИЦИПАЛЬНОЕ АВТОНОМНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 2

Подготовил

Легкоконец Владислав, ученик 10А класса

Практическое применение Теории Графов

Руководитель

Л.И. Носкова, учитель математики

ст.Брюховецкая

2011 г.

1.Введение………………………………………………………………………….………….3

2.История возникновения теории графов………………………………………….………..4

3.Основные определения и теоремы теории графов……………………………….………6

4.Задачи,решаемые при помощи графов……………………………..……………………..8

4.1 Знаменитые задачи………………………………….………………………...8

4.2 Несколько интересных задач………………………………….……………..9

5.Применение графов в различных областях жизни людей……………………………...11

6.Решение задач……………………………………………………………………………...12

7. Заключение………………….…………………………………………………………….13

8. Список литературы………….……………………………………………………………14

9.Приложение…………………………………………………………………….…………15

Введение

Родившись при решении головоломок и занимательных игр, теория графов стала в настоящее время простым, доступным и мощным средством решения вопросов, относящихся к широкому кругу проблем. Графы буквально вездесущи. В виде графов можно, например, интерпретировать схемы дорог и электрические цепи, географические карты и молекулы химических соединений, связи между людьми и группами людей. За последние четыре десятилетия теория графов превратилась в один из наиболее бурно развивающихся разделов математики. Это вызвано запросами стремительно расширяющейся области приложений. Применяется при проектировании интегральных схем и схем управления, при исследовании автоматов, логических цепей, блок- схем программ, в экономике и статистике, химии и биологии, в теории расписаний. Поэтому актуальность темы обусловлена с одной стороны популярностью графов и связанных с ними методов исследований, а с другой, не разработанная, целостная система ее реализации.

Решение многих жизненных задач требует длинных вычислений, а иногда и эти вычисления не приносят успеха. В этом и состоит проблема исследования . Возникает вопрос: нельзя ли для их решения найти простое, рациональное, короткое и изящное решение. Упрощается ли решение задач, если использовать графы? Это определило тему моего исследования : «Практическое применение теории графов»

Целью исследования было с помощью графов научиться быстро решать практические задачи.

Гипотеза исследования. Метод графов очень важен и широко применяется в различных областях науки и жизнедеятельности человека.

Задачи исследования:

1.Изучить литературу и ресурсы сети Интернет по данной проблеме.

2.Проверить эффективность метода графов при решении практических задач.

3. Сделать вывод.

Практическая значимость исследования заключается в том, что результаты несомненно вызовут интерес у многих людей. Разве не пытался кто-то из вас построить генеалогическое дерево своей семьи? А как это сделать грамотно? Руководителю транспортного предприятия наверняка приходится решать проблему более выгодного использования транспорта при перевозке грузов с места назначения в несколько населенных пунктов. Каждый школьник сталкивался с логическими задачами на переливание. Оказывается они решаются при помощи графов легко.

В работе используются следующие методы: наблюдение, поиск, отбор, анализ.

История возникновения теории графов

Родоначальником теории графов принято считать математика Леонарда Эйлера (1707-1783). Историю возникновения этой теории можно проследить по переписке великого ученого. Вот перевод латинского текста, который взят из письма Эйлера к итальянскому математику и инженеру Маринони, отправленного из Петербурга 13 марта 1736 года.

"Некогда мне была предложена задача об острове, расположенном в городе Кенигсберге и окруженном рекой, через которую перекинуто семь мостов.

[Приложение рис.1] Спрашивается, может ли кто-нибудь непрерывно обойти их, проходя только однажды через каждый мост. И тут же мне было сообщено, что никто еще до сих пор не мог это проделать, но никто и не доказал, что это невозможно. Вопрос этот, хотя и банальный, показался мне, однако, достойным внимания тем, что для его решения недостаточны ни геометрия, ни алгебра, ни комбинаторное искусство. После долгих размышлений я нашел легкое правило, основанное на вполне убедительном доказательстве, с помощью которого можно во всех задачах такого рода тотчас же определить, может ли быть совершен такой обход через какое угодно число и как угодно расположенных мостов или не может. Кенигсбергские же мосты расположены так, что их можно представить на следующем рисунке [Приложение рис.2] , на котором A обозначает остров, а B ,C иD – части континента, отделенные друг от друга рукавами реки

По поводу обнаруженного им способа решать задачи подобного рода Эйлер писал:

"Это решение по своему характеру, по-видимому, имеет мало отношения к математике, и мне непонятно, почему следует скорее от математика ожидать этого решения, нежели от какого-нибудь другого человека, ибо это решение подкрепляется одним только рассуждением, и нет необходимости привлекать для нахождения этого решения какие-либо законы, свойственные математике. Итак, я не знаю, каким образом получается, что вопросы, имеющие совсем мало отношения к математике, скорее разрешается математиками, чем другими".

Так можно ли обойти Кенигсбергские мосты, проходя только один раз через каждый из этих мостов? Чтобы найти ответ, продолжим письмо Эйлера к Маринони:

"Вопрос состоит в том, чтобы определить, можно ли обойти все эти семь мостов, проходя через каждый только однажды, или нельзя. Мое правило приводит к следующему решению этого вопроса. Прежде всего, нужно смотреть, сколько есть участков, разделенных водой, – таких, у которых нет другого перехода с одного на другой, кроме как через мост. В данном примере таких участков четыре – A , B , C , D . Далее нужно различать, является ли число мостов, ведущих к этим отдельным участкам, четным или нечетным. Так, в нашем случае к участку A ведут пять мостов, а к остальным – по три моста, т. е. Число мостов, ведущих к отдельным участкам, нечетно, а этого одного уже достаточно для решения задачи. Когда это определено, применяем следующее правило: если бы число мостов, ведущих к каждому отдельному участку, было четным, то тогда обход, о котором идет речь, был бы возможен, и в то же время можно было бы начать этот обход с любого участка. Если же из этих чисел два были бы нечетные, ибо только одно быть нечетным не может, то и тогда мог бы совершиться переход, как это предписано, но только начало обхода непременно должно быть взято от одного из тех двух участков, к которым ведет нечетное число мостов. Если бы, наконец, было больше двух участков, к которым ведет нечетное число мостов, то тогда такое движение вообще невозможно… если можно было привести здесь другие, более серьезные задачи, этот метод мог бы принести еще большую пользу и им не следовало бы пренебрегать".

Основные определения и теоремы теории графов

Теория графов – дисциплина математическая, созданная усилиями математиков, поэтому ее изложение включает в себя и необходимые строгие определения. Итак, приступим к организованному введению основных понятий этой теории.

Определение 1. Графомназывается совокупность конечного числа точек, называемых вершинами графа, и попарно соединяющих некоторые из этих вершин линий, называемых ребрамиили дугами графа.

Это определение можно сформулировать иначе: графомназывается непустое множество точек (вершин) и отрезков (ребер), оба конца которых принадлежат заданному множеству точек

В дальнейшем вершины графа мы будем обозначать латинскими буквами A , B , C , D . Иногда граф в целом будем обозначать одной заглавной буквой.

Определение 2. Вершины графа, которые не принадлежат ни одному ребру, называются изолированными.

Определение 3. Граф, состоящий только из изолированных вершин, называется нуль- графом.

Обозначение: O "– граф с вершинами, не имеющий ребер

Определение 4. Граф, в котором каждая пара вершин соединена ребром, называется полным.

Обозначение: U " – граф, состоящий из n вершин и ребер, соединяющих всевозможные пары этих вершин. Такой граф можно представить как n –угольник, в котором проведены все диагонали

Определение 5. Степеньювершиныназывается число ребер, которым принадлежит вершина.

Определение 6. Граф, степени всех k вершин которого одинаковы, называется однороднымграфомстепениk .

Определение 7. Дополнениемданногографаназывается граф, состоящий из всех ребер и их концов, которые необходимо добавить к исходному графу, чтобы получить полный граф.

Определение 8. Граф, который можно представить на плоскости в таком виде, когда его ребра пересекаются только в вершинах, называется плоским.

Определение 9. Многоугольник плоского графа, не содержащий внутри себя никаких вершин или ребер графа, называют его гранью.

Понятия плоского графа и грани графа применяется при решении задач на "правильное" раскрашивание различных карт.

Определение 10. Путемот A доX называется последовательность ребер, ведущая от A к X , такая, что каждые два соседних ребра имеют общую вершину, и никакое ребро не встречается более одного раза.

Определение 11. Цикломназывается путь, в котором совпадают начальная и конечная точка.

Определение 12. Простым цикломназывается цикл, не проходящий ни через одну из вершин графа более одного раза.

Определение 13. Длиной пути, проложенного на цикле, называется число ребер этого пути.

Определение 14. Две вершины A и B в графе называются связными(несвязными), если в нем существует (не существует) путь, ведущий из A в B .

Определение 15. Граф называется связным, если каждые две его вершины связны; если же в графе найдется хотя бы одна пара несвязных вершин, то граф называется несвязным.

Определение 16. Деревомназывается связный граф, не содержащий циклов.

Трехмерной моделью графа-дерева служит, например, настоящее дерево с его замысловато разветвленной кроной; река и ее притоки также образуют дерево, но уже плоское – на поверхности земли.

Определение 17. Несвязный граф, состоящий исключительно из деревьев, называется лесом.

Определение 18. Дерево, все n вершин которого имеют номера от 1 до n , называют деревом с перенумерованными вершинами.

Итак, мы рассмотрели основные определения теории графов, без которых было бы невозможно доказательство теорем, а, следовательно и решение задач.

Задачи решаемые при помощи графов

Знаменитые задачи

Задача коммивояжера

Задача коммивояжера является одной из знаменитых задач теории комбинаторики. Она была поставлена в 1934 году, и об неё обламывали зубы лучшие математики.

Постановка задачи следующая.
Коммивояжер (бродячий торговец) должен выйти из первого города, посетить по разу в неизвестном порядке города 2,1,3..n и вернуться в первый город. Расстояния между городами известны. В каком порядке следует обходить города, чтобы замкнутый путь (тур) коммивояжера был кратчайшим?

Метод решения задачи коммивояжера

Жадный алгоритм “иди в ближайший (в который еще не входил) город”.
“Жадным” этот алгоритм назван потому, что на последних шагах приходится жестоко расплачиваться за жадность.
Рассмотрим для примера сеть на рисунке [приложение рис.3] , представляющую узкий ромб. Пусть коммивояжер стартует из города 1. Алгоритм “иди в ближайший город” выведет его в город 2, затем 3, затем 4; на последнем шаге придется платить за жадность, возвращаясь по длинной диагонали ромба. В результате получится не кратчайший, а длиннейший тур.

Задача о Кенигсбергских мостах.

Задача формулируется следующим образом.
Город Кенигсберг расположен на берегах реки Прегель и двух островах. Различные части города были соединены семью мостами. По воскресеньям горожане совершали прогулки по городу. Вопрос: можно ли совершить прогулку таким образом, чтобы, выйдя из дома, вернуться обратно, пройдя в точности один раз по каждому мосту.
Мосты через реку Прегель расположены как на рисунке [приложение Рис.1].

Рассмотрим граф, соответствующий схеме мостов [приложение рис.2].

Чтобы ответить на вопрос задачи, достаточно выяснить, является ли граф эйлеровым. (Хотя бы из одной вершины должно выходить четное число мостов). Нельзя, прогуливаясь по городу, пройти по одному разу все мосты и вернуться обратно.

Несколько интересных задач

1. "Маршруты".

Задача 1

Как вы помните, охотник за мертвыми душами Чичиков побывал у известных помещиков по одному разу у каждого. Он посещал их в следующем порядке: Манилова, Коробочку, Ноздрева, Собакевича, Плюшкина, Тентетникова, генерала Бетрищева, Петуха, Констанжолго, полковника Кошкарева. Найдена схема, на которой Чичиков набросал взаимное расположение имений и проселочных дорог, соединяющих их. Установите, какое имение кому принадлежит, если ни одной из дорог Чичиков не проезжал более одного раза [приложение рис.4].

Решение :

По схеме дорог видно, что путешествие Чичиков начал с имения Е, а окончил имением О. Замечаем, что в имения В и С ведут только две дороги, поэтому по этим дорогам Чичиков должен был проехать. Отметим их жирной линией. Определены участки маршрута, проходящие через А: АС и АВ. По дорогам АЕ, АК и АМ Чичиков не ездил. Перечеркнем их. Отметим жирной линией ЕD ; перечеркнем DK . Перечеркнем МО и МН; отметим жирной линией MF ; перечеркнем FO ; отметим жирной линией FH , НК и КО. Найдем единственно возможный при данном условии маршрут. И получаем: имение Е – принадлежит Манилову, D - Коробочке, С – Ноздреву, А – Собакевичу, В – Плюшкину, М – Тентетникову, F - Бетрищеву, Н – Петуху, К – Констанжолго, О – Кошкареву [приложение рис.5] .

Задача 2

На рисунке изображена схема местности [приложение рис.6].

Передвигаться можно только в направлении стрелок. В каждом пункте можно бывать не более одного раза. Сколькими способами можно попасть из пункта 1 в пункт 9? Какой маршрут самый короткий и какой - самый длинный.

Решение :

Последовательно "расслаиваем" схему в дерево, начиная с вершины 1[приложение рис.7] . Получим дерево. Число возможных способов попадания из 1 в 9 равно числу "висячих" вершин дерева (их 14). Очевидно, кратчайший путь-1-5-9; самый длинный - 1-2-3-6-5-7-8-9.

2 "Группы, знакомства"

Задача 1

Участники музыкального фестиваля, познакомившись, обменялись конвертами с адресами. Докажите, что:

а) всего было передано четное число конвертов;

б) число участников, обменявшихся конвертами нечетное число раз, четно.

Решение: Пусть участники фестиваля А 1 , А 2 , А 3 . . . , А n – вершины графа, а ребра соединяют пары вершин, изображающих ребят, обменявшихся конвертами [Приложение рис.8]

Решение:

а) степень каждой вершины А i показывает число конвертов, которое передал участник А i своим знакомым. Общее число переданных конвертов N равно сумме степеней всех вершин графа N = степ. А 1 + степ. А 2 + + . . . + степ. А n -1 + степ. А n , N =2p , где p – число ребер графа, т.е. N – четное. Следовательно, было передано четное число конвертов;

б) в равенстве N = степ. А 1 + степ. А 2 + + . . . + степ. А n -1 + степ. А n сумма нечетных слагаемых должна быть четной, а это может быть только в том случае, если число нечетных слагаемых четно. А это означает, что число участников, обменявшихся конвертами нечетное число раз, четное.

Задача 2

Однажды Андрей, Борис, Володя, Даша и Галя договорились вечером пойти в кино. Выбор кинотеатра и сеанса они решили согласовать по телефону. Было также решено, что если с кем-то созвониться не удастся, то поход в кино отменяется. Вечером у кинотеатра собрались не все, и поэтому посещение кино сорвалось. На следующий день стали выяснять, кто кому звонил. Оказалось, что Андрей звонил Борису и Володе, Володя звонил Борису и Даше, Борис звонил Андрею и Даше, Даша звонила Андрею и Володе, а Галя звонила Андрею, Володе и Борису. Кто не сумел созвониться и поэтому не пришёл на встречу?

Решение:

Нарисуем пять точек и обозначим их буквами А, Б, В, Г, Д. Это первые буквы имён. Соединим те точки, которые соответствуют именам созвонившихся ребят.

[ приложение рис.9]

Из рисунка видно, что каждый из ребят – Андрей, Борис и Володя - созвонились со всеми остальными. Поэтому эти ребята и пришли к кинотеатру. А Галя и Даша не сумели созвониться между собой (точки Г и Д не соединены отрезком) и поэтому в соответствии с договорённостью в кино не пришли.

Применение графов в различных областях жизни людей

Кроме приведенных примеров, графы широко используются в строительстве, электротехнике, менеджменте, логистике, географии, машиностроении, социологии, программировании, автоматизации технологических процессов и производств, психологии, рекламе. Итак, из всего вышесказанного неопровержимо следует практическая ценность теории графов, доказательство которой и являлось целью данного исследования.

В любой области науки и техники встречаешься с графами. Графы - это замечательные математические объекты, с помощью которых можно решать математические, экономические и логические задачи, различные головоломки и упрощать условия задач по физике, химии, электронике, автоматике. Многие математические факты удобно формулировать на языке графов. Теория графов является частью многих наук. Теория графов - одна из самых красивых и наглядных математических теорий. В последнее время теория графов находит всё больше применений и в прикладных вопросах. Возникла даже компьютерная химия - сравнительно молодая область химии, основанная на применении теории графов.

Молекулярные графы , применяемые в стереохимии и структурной топологии, химии кластеров, полимеров и др., представляют собой неориентированные графы, отображающие строение молекул [приложение рис.10] . Вершины и ребра этих графов отвечают соответственным атомам и химическим связям между ними.

Молекулярные графы и деревья: [приложение рис.10] а, б - мультиграфы соотв. этилена и формальдегида; в-мол. изомеров пентана (деревья 4, 5 изоморфны дереву 2).

В стереохимии организмов наиболее. часто используют молекулярные деревья -основные деревья молекулярных графов, которые содержат только все вершины, соответствующие атомам С. Составление наборов мол. деревьев и установление их изоморфизма позволяют определять мол. структуры и находить полное число изомеров алканов, алкенов и алкинов

Белковые сети

Белковые сети - группы физически взаимодействующих белков, которые функционируют в клетке совместно и скоординированно, контролируя взаимосвязанные процессы, происходящие в организме [приложение рис. 11].

Граф иерархической системы называется деревом. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь. Дерево не содержит циклов и петель.

Обычно у дерева, представляющего иерархическую систему, выделяется одна главная вершина, которая называется корнем дерева. Каждая вершина дерева (кроме корня) имеет только одного предка – обозначенный ею объект входит в один класс верхнего уровня. Любая вершина дерева может порождать несколько потомков – вершин, соответствующих классам нижнего уровня.

Для каждой пары вершин дерева существует единственный путь, их соединяющий. Этим свойством пользуются при нахождении всех предков, например, по мужской линии, любого человека, чья родословная представлена в виде генеалогического дерева, которое является «деревом» и в смысле теории графов.

Пример генеалогического дерева моей семьи [приложение рис.12].

Еще один пример. На рисунке показано библейское генеалогическое дерево [приложение рис.13].

Решение задач

1.Транспортная задача . Пусть в городе Краснодаре находится база с сырьём, которое нужно развести по городам Крымск, Темрюк, Славянск-на-Кубани и Тимашевск одним заездом, затратив при этом как можно меньше времени и топлива и вернувшись обратно в Краснодар.

Решение:

Для начала составим граф всех возможных путей проезда [приложение рис.14] , учитывая реальные дороги между данными населенными пунктами и расстояние между ними. Для решения этой задачи нам потребуется составить еще один граф, древовидный [приложение рис.15] .

Для удобства решения обозначаем города цифрами: Краснодар – 1, Крымск – 2, Темрюк – 3, Славянск – 4, Тимашевск – 5.

В результате вышло 24 решения, но нам нужны только кратчайшие пути. Из всех решений удовлетворяют только два, это 350 км.

Подобно этому можно и, я думаю, нужно рассчитывать реальные перевозки из одного населенного пункта в другие.

Логическая задача на переливание. В ведре 8 л воды, и имеется две кастрюли емкостью 5 и 3 л. требуется отлить в пятилитровую кастрюлю 4 л воды и оставить в ведре 4 л, т. е. разлить воду поровну в ведро и большую кастрюлю.

Решение:

Ситуацию в каждый момент можно описать тремя числами [приложение рис.16].

В результате получаем два решения: одно в 7 ходов, другое в 8 ходов.

Заключение

Итак, для того чтобы научиться решать задачи, надо разобраться в том, что собой они представляют, как они устроены, из каких составных частей они состоят, каковы инструменты, с помощью которых производится решение задач.

Решая практические задачи с помощью теории графов стало ясно видно, что в каждом шаге, в каждом этапе их решения необходимо применить творчество.

С самого начала, на первом этапе, оно заключается в том, что нужно суметь проанализировать и закодировать условие задачи. Второй этап – схематическая запись, которая состоит в геометрическом представлении графов, и на этом этапе элемент творчества очень важен потому, что далеко не просто найти соответствия между элементами условия и соответствующими элементами графа.

Решая транспортную задачу или задачу на составление генеалогического дерева я сделал вывод, что безусловно метод графов интересен, красив и нагляден.

Я убедился, что графы достаточно широко применяются в экономике, управлении, технике. Также теория графов применяется в программировании.Об этом в данной работе не шла речь, но думаю, что это только вопрос времени.

В настоящей научной работе рассмотрены математические графы, области их применения, решено несколько задач с помощью графов. Знание основ теории графов необходимо в различных областях, связанных с управлением производством, бизнесом (например, сетевой график строительства, графики доставки почты). Кроме того, работая над научной работой, я освоил работу на компьютере в текстовом редакторе WORD . Таким образом, задачи научной работы выполнены.

Итак, из всего вышесказанного неопровержимо следует практическая ценность теории графов, доказательство которой и являлось целью данной работы.

Литература

Берж К. Теория графов и ее применения. -M.: ИИЛ, 1962.

Кемени Дж., Снелл Дж., Томпсон Дж. Введение в конечную математику. -M.: ИИЛ, 1963.

Оре О. Графы и их применение. -M.: Мир, 1965.

Харари Ф. Теория графов. -M.: Мир, 1973.

Зыков А.А. Теория конечных графов. -Новосибирск: Наука, 1969.

Березина Л.Ю. Графы и их применение. -M.: Просвещение, 1979. -144 c.

"Соросовский образовательный журнал" №11 1996 (ст. "Плоские графы");

Гарднер М. "Математические досуги", М. "Мир", 1972(глава 35);

Олехник С. Н., Нестеренко Ю. В., Потапов М. К. "Старинные занимательные задачи", М. "Наука", 1988(часть 2, раздел 8; приложение 4);

Приложение

Приложение

П

Рис. 6

Рис. 7

Рис. 8

риложение

Приложение

Приложение

Приложение

П

Рис. 14

риложение

Приложение

Виды графов могут определяться общими принципами их построения (таковы, например, двудольный граф и эйлеров граф), а могут зависеть от тех или иных свойств вершин или рёбер (например, ориентированный и неориентированный граф, обыкновенный граф).

Ориентированные и неориентированные графы

звеньями (порядок двух концов ребра графа не существенен), называются неориентированными .

Графы, в которых все рёбра являются дугами (порядок двух концов ребра графа существенен), называются ориентированными графами или орграфами .

Неориентированный граф может быть представлен в виде ориентированного графа , если каждое его звено заменить на две дуги, имеющие противоположные направления.

Графы с петлями, смешанные графы, пустые графы, мультиграфы, обыкновенные графы, полные графы

Если граф содержит петли , то это обстоятельство специально оговаривают, добавляя к основной харатеристике графа слова "с петлями", например, "орграф с петлями". Если граф не содержит петель, то добавляют слова "без петель".

Смешанным называют граф, в котором имеются рёбра хотя бы двух из упомянутых трёх разновидностей (звенья, дуги, петли).

Граф, состоящий только из голых вершин , называется пустым .

Мультиграфом называется граф, в котором пары вершин могут быть соединены более чем одним ребром, то есть содершащий кратные рёбра , но не содержащий петель.

Граф без дуг (то есть неориентированный), без петель и кратных рёбер называется обыкновенным . Обыкновенный граф изображён на рисунке ниже.

Граф заданного типа называют полным , если он содержит все возможные для этого типа рёбра (при неизменном множестве вершин). Так, в полном обыкновенном графе каждая пара различных вершин соединена ровно одним звеном (рисунок ниже).

Двудольный граф

Граф называется двудольным , если множество его вершин можно разбить на два подмножества так, чтобы никакое ребро не соединяло вершины одного и того же подмножества.

Пример 1. Построить полный двудольный граф.

Полный двудольный граф состоит из двух множеств вершин и из всевозможных звеньев, соединяющих вершины одного множества с вершинами другого множества (рисунок ниже).

Эйлеров граф

Мы уже касались задачи о кёнигсбергских мостах . Отрицательное решение Эйлером этой задачи привело к первой опубликованной работе по теории графов. Задачу об обходе мостов можно обобщить и получить следующую задачу теории графов: можно ли найти в данной графе цикл, содержащий все вершины и все рёбра? Граф, в котором это возможно, называется эйлеровым графом.

Итак, эйлеровым графом называется граф, в котором можно обойти все вершины и при этом пройти одно ребро только один раз. В нём каждая вершина должна иметь только чётное число рёбер.

Пример 2. Является ли полный граф с одинаковым числом n рёбер, которым инцидентна каждая вершина, эйлеровым графом? Объяснить ответ. Привести примеры.

Ответ. Если n - нечётное число, то каждая вершина инцидентна n -1 рёбрам. В таком случае данный граф является эйлеровым графом. Примеры таких графов на рисунке ниже.

Регулярный граф

Регулярным графом называется связный граф, все вершины которого имеют одинаковую степень k . Таким образом, на рисунке к примеру 2 изображены примеры регулярных графов, называемых по степени его вершин 4-регулярными и 2-регулярными графами или регулярными графами 4-й степени и 2-й степени.

Число вершин регулярного графа k -й степени не может быть меньше k +1. У регулярного графа нечётной степени может быть лишь чётное число вершин.

Пример 3. Построить регулярный граф, в котором самый короткий цикл имеет длину 4.

Решение. Рассуждаем так: для того, чтобы длина цикла удовлетворяла заданному условию, требуется, чтобы число вершин графа было кратно четырём. Если число вершин равно четырём, то получится граф, изображённый на рисунке ниже. Он является регулярным, но в нём самый короткий цикл имеет длину 3.

Увеличиваем число вершин до восьми (следующее число, кратное четырём). Соединяем вершины рёбрами так, чтобы степени вершин были равны трём. Получаем следующий граф, удовлетворяющий условиям задачи.

Гамильтонов граф

Гамильтоновым графом называется граф, содержащий гамильтонов цикл. Гамильтоновым циклом называется простой цикл, проходящий через все вершины рассматриваемого графа. Таким образом, говоря проще, гамильтонов граф - это такой граф, в котором можно обойти все вершины и каждая вершина при обходе повторяется лишь один раз. Пример гамильтонова графа - на рисунке ниже.

Пример 4. Задан двудольный граф, в котором n - число вершин из множества A , а m - число вершин из множества B . В каком случае граф будет эйлеровым графом, а в каком случае - гамильтоновым графом?

Перед тем как начать изучение непосредственно алгоритмов, необходимо обладать базовыми знаниями касательно самих графов, понимать, как они представляются в компьютере. Здесь не будут подробно описаны все аспекты теории графов (этого и не требуется), но только те, незнание которых заметно усложнит усвоение данной области программирования.

Несколько примеров дадут немного поверхностного представления о графе. Так типичным графом является схема метро или какой-либо другой маршрут. В частности программисту знакома компьютерная сеть, также являющаяся графом. Общее здесь это наличие точек, соединенных линиями. Так в компьютерной сети точки – это отдельные серверы, а линии – различные виды электрических сигналов. В метрополитене первое – станции, второе – туннели, проложенные между ними. В теории графов точки именуется вершинами (узлами ), а линии – ребрами (дугами ). Таким образом, граф – это совокупность вершин, соединённых ребрами.

Математика оперирует не содержанием вещей, а их структурой, абстрагируя ее из всего того, что дано как целое. Пользуясь именно этим приемом, мы можем заключать о каких-либо объектах как о графах. А поскольку теория графов это часть математики, то для нее нет абсолютно никакого значения, что в принципе представляет собой объект; важно лишь то, является ли он графом, т. е. обладает ли обязательными для графов свойствами. Поэтому, прежде чем привести примеры, мы выделяем в рассматриваемом объекте лишь то, что как нам кажется, позволит показать аналогию, отыскиваем общее.

Вернемся к компьютерной сети. Она обладает определенной топологией, и может быть условно изображена в виде некоторого числа компьютеров и путей их соединяющих. На рисунке ниже в качестве примера показана полносвязная топология.

Это по сути граф. Пять компьютеров являются вершинами, а соединения (пути передачи сигналов) между ними – ребрами. Заменив компьютеры вершинами, мы получим математический объект – граф, который имеет 10 ребер и 5 вершин. Пронумеровать вершины можно произвольным образом, а не обязательно так, как это сделано на рисунке. Стоит отметить, что в данном примере не используется ни одной петли, то есть такого ребра, которое выходит из вершины и сразу же входит в нее, но петли могут встречаться в задачах.

Вот некоторые важные обозначения, используемые в теории графов:

• G=(V, E), здесь G – граф, V – его вершины, а E – ребра;
• |V| – порядок (число вершин);
• |E| – размер графа (число рёбер).

В нашем случае (рис. 1) |V|=5, |E|=10;

Когда из любой вершины доступна любая другая вершина, то такой граф называется неориентированным связным графом (рис. 1). Если же граф связный, но это условие не выполняется, тогда такой граф называется ориентированным или орграфом (рис. 2).

В ориентированных и неориентированных графах имеется понятие степени вершины. Степень вершины – это количество ребер, соединяющих ее с другими вершинами. Сумма всех степеней графа равна удвоенному количеству всех его ребер. Для рисунка 2 сумма всех степеней равна 20.

В орграфе, в отличие от неориентированного графа, имеется возможность двигаться из вершины h в вершину s без промежуточных вершин, лишь тогда когда ребро выходит из h и входит в s, но не наоборот.

Ориентированные графы имеют следующую форму записи:

G=(V, A), где V – вершины, A – направленные ребра.

Третий тип графов – смешанные графы (рис. 3). Они имеют как направленные ребра, так и ненаправленные. Формально смешанный граф записывается так: G=(V, E, A), где каждая из букв в скобках обозначает тоже, что ей приписывалось ранее.

В графе на рисунке 3 одни дуги направленные [(e, a), (e, c), (a, b), (c, a), (d, b)], другие – ненаправленные [(e, d), (e, b), (d, c)…].

Два или более графов на первый взгляд могут показаться разными по своей структуре, что возникает вследствие различного их изображения. Но это не всегда так. Возьмем два графа (рис. 4).

Они эквивалентны друг другу, ведь не изменяя структуру одного графа можно построить другой. Такие графы называются изоморфными , т. е. обладающими тем свойством, что какая-либо вершина с определенным числом ребер в одном графе имеет тождественную вершину в другом. На рисунке 4 изображены два изоморфных графа.

Когда каждому ребру графа поставлено в соответствие некоторое значение, называемое весом ребра, тогда такой граф взвешенный . В разных задачах в качестве веса могут выступать различные виды измерений, например длины, цены маршруты и т. п. В графическом представлении графа весовые значения указываются, как правило, рядом с ребрами.

В любом из рассмотренных нами графов имеется возможность выделить путь и, причем не один. Путь – это последовательность вершин, каждая из которых соединена с последующей посредством ребра. Если первая и последняя вершины совпадают, то такой путь называется циклом. Длина пути определяется количеством составляющих его ребер. Например, на рисунке 4.а путем служит последовательность [(e), (a), (b), (c)]. Этот путь является подграфом, так как к нему применимо определение последнего, а именно: граф G’=(V’, E’) является подграфом графа G=(V, E), только тогда когда V’ и E’ принадлежат V, E.